This works!
but, when compared to the better solutions to come, is wasteful of resourses and hence is

• slower
• hotter
• bigger
• all these are bad

The product register must be 64 bits since the product is 64 bits

Why is multiplicand register 64 bits?

• So that we can shift it left
• I.e., for our convenience.
  By this I mean it is not required by the problem specification,
  but only by the solution method chosen.

Why is ALU 64-bits?

• Because the product is 64 bits
• But we are only adding a 32-bit quantity to the product at any one step.
• Hmmm.
• Maybe we can just pull out the correct bits from the product.
• Would be tricky to pull out bits in the middle because which bits to pull changes each step

POOF!! ... as the smoke clears we see an idea.

We can solve both problems at once

• DON'T shift the multiplicand left
  • Hence register is 32-bits.
  • Also register need not be a shifter
  
  
• Instead shift the product right!
  
  
• Add the high-order (HO) 32-bits of product register to multiplicand and place result back into HO 32-bits
  • Only do this if the current multiplier bit is one.
    
    
  • Use the Carry Out of the sum as the new bit to shift in
    
    
  • The book forgot the last point but their example used numbers too small to generate a carry

This results in the following algorithm

    product <- 0
    for i = 0 to 31
        if LOB of multiplier = 1
            (serial_in, product[32-63]) <- product[32-63] + multiplicand
        shift product right 1 bit
        shift multiplier right 1 bit

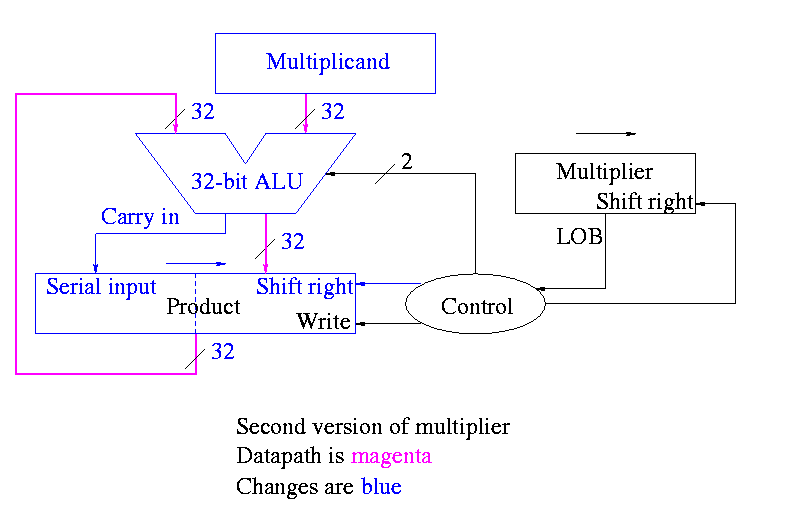
What about control

• Just as boring as before
• Send (ADD, 1, 1) to (ALU, multiplier (shift right), Product (shift right))
• Send LOB to Product (write)

Redo same example on board

A final trick (``gate bumming'', like code bumming of 60s)

• There is a waste of registers, i.e. not full unilization
  • The multiplicand is fully unilized since we always need all 32 bits
  • But once we use a multiplier bit, we can toss it so we need less and less of the multiplier as we go along
  • And the product is half unused at beginning and only slowly ...
  • POOF!!
  
  
• ``Timeshare'' the LO half of the ``product register''
  • In the beginning LO half contains the multiplier
  • Each step we shift right and more goes to product less to multiplier
  
  
• The algorithm changes to

    product[0-31] <- multiplier
    for i = 0 to 31
        if LOB of product = 1
            (serial_in, product[32-63]) <- product[32-63] + multiplicand
        shift product right 1 bit

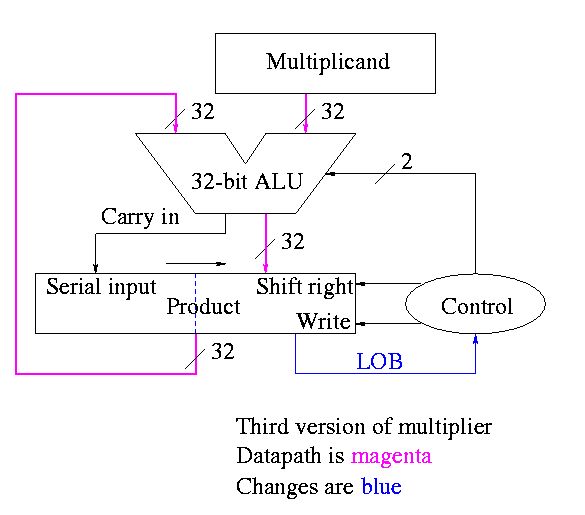
Control again boring

• Send (ADD, 1) to (ALU, Product (shift right))
• Send LOB to Product (write)

Redo same example on board

The above was for unsigned 32-bit multiplication

For signed multiplication

• Save the signs of the multiplier and multiplicand
• Convert multiplier and multiplicand to non-neg numbers
• Use above algorithm
• Only use 31 steps not 32 since there are only 31 multiplier bits (the HOB of the multiplier is the sign bit, not a bit used for multiplying)
• Compliment product if original signs were different

There are faster multipliers, but we are not covering them.

We are skiping division.

We are skiping floating point.

Homework: Read 4.11 ``Historical Perspective''.