As noted just above the tall skinny box is useful for all size CLAs. To expand on that point and to review CLAs, let's redo CLAs with the general box.

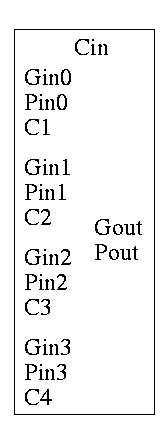
Since we are doing 4-bits at a time, the box takes 9=2*4+1 input bits and produces 6=4+2 outputs

• Inputs
  • 4 generate bits from the previous size (i.e. if now doing a 64-bit CLA, these are the generate bits from the four 16-bit CLAs). Let's call these bits Gin0, Gin1, Gin2, Gin3.
  • 4 propogate bits from the previous size Pin0, Pin1, Pin2, Pin3.
  • The Carry in Cin
  
  
• Outputs
  • Four carries C1, C2, C3, and C4 to be used in the previous size
    • Cin is also called C0 and is used in the previous size as well as in this box.
    • C4 is also called Cout. It is the carry out from this size, but is not used in the next size
  • Gout and Pout, the generate and propogate to be used in the next size
  
  
• Formulas

  C1 = G0 + PO Cin
  C2 = G1 + P1 G0 + P1 P0 Cin
  C3 = G2 + P2 G1 + P2 P1 G0 + P2 P1 P0 Cin
  C4 = G3 + P3 G2 + P3 P2 G1 + P3 P2 P1 G0 + P3 P2 P1 P0 Cin
  
  Gout = G3  +  P3 G2  +  P3 P2 G1  +  P3 P2 P1 Go
  Pout = P3 P2 P1 P0
  
  

• Picture

  

A 4-bit adder is now

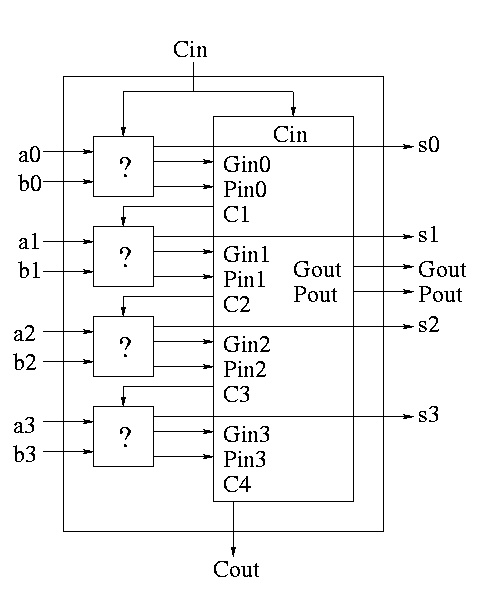
What does the ``?'' box do?

• Calculates Gi and Pi based on ai and bi
  • Gi = ai bi
  • Pi = ai + bi
  
  
• Calculate s1 based on ai, bi, and Ci=Cin (normal full adder)
  
  
• Do not bother calculating Cout

Now take four of these 4-bit adders and use the identical CLA box to get a 16-bit adder

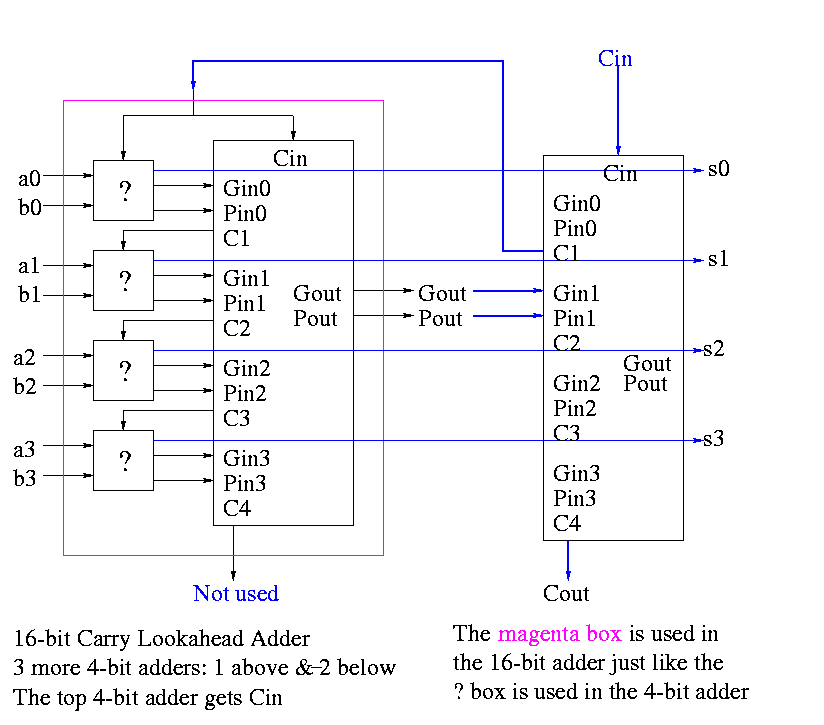
Four of these 16-bit adders with the identical CLA box to gives a 64-bit adder.

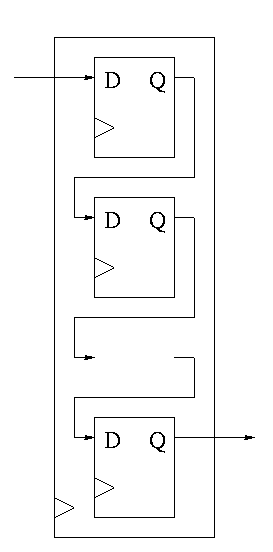
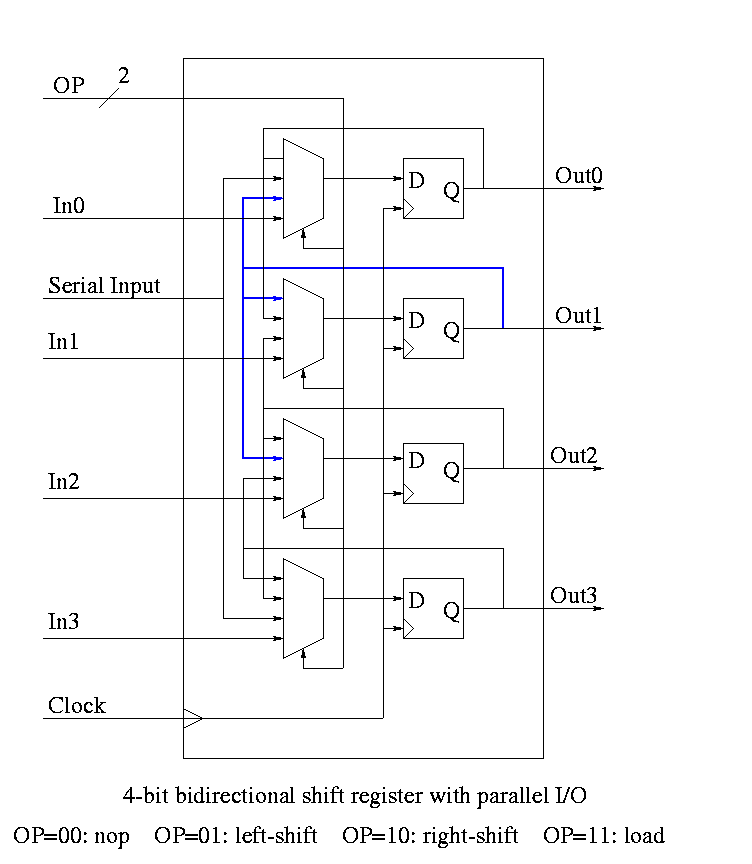
Shifter

• Just a string of D-flops; output of one is input of next
  • Input to first is the serial input.
  • Output of last is the serial output.

    

  
  
• We want more.
  • Left and right shifting (with serial input/output)
  • Parallel load
  • Parallel Output
  • Don't shift every cycle
• Parallel output is just wires.
• Shifter has 4 modes (left-shift, right-shift, nop, load) so
  • 4-1 mux inside
  • 2 control lines must come in

  

• We could modify our registers to be shifters (bigger mux), but ...
• Our shifters are slow for big shifts; ``barrel shifters'' are better

Homework: A 4-bit shift register initially contains 1101. It is shifted six times to the right with the serial input being 101101. What is the contents of the register after each shift.

Homework: Same register, same init condition. For the first 6 cycles the opcodes are left, left, right, nop, left, right and the serial input is 101101. The next cycle the register is loaded (in parallel) with 1011. The final 6 cycles are the same as the first 6. What is the contents of the register after each cycle?

Multipliers

• Recall how to do multiplication.
  • Multiplicand times multiplier gives product
  • Multiply multiplicand by each digit of multiplier
  • Put the result in the correct column
  • Then add the partial products just produced
  
  
• We will do it the same way ...
  ... but differently
  
  
  • We are doing binary arithmetic so each ``digit'' of the multiplier is 1 or zero.
    
    
  • Hence ``multiplying'' the mulitplicand by a digit of the multiplier means either
    • Getting the multiplicand
    • Getting zero
    
    
  • Use an ``if appropriate bit of multiplier is 1'' stmt
    
    
  • To get the ``appropriate bit''
    • Start with the LOB of the multiplier
    • Shift the multiplier right (so the next bit is the LOB)
    
    
  • Putting in the correct column means putting it one column further left that the last time.
    
    
  • This is done by shifting the multiplicand left one bit each time (even if the multiplier bit is zero)
    
    
  • Instead of adding partial products at end, keep a running sum
    • If the multiplier bit is zero add the (shifted) multiplicand to the running sum
    • If the bit is zero, simply skip the addition.
  
  
• This results in the following algorithm

    product <- 0
    for i = 0 to 31
        if LOB of multiplier = 1
            product = product + multiplicand
        shift multiplicand left 1 bit
        shift multiplier right 1 bit

Do on board 4-bit addition (8-bit registers) 1100 x 1101

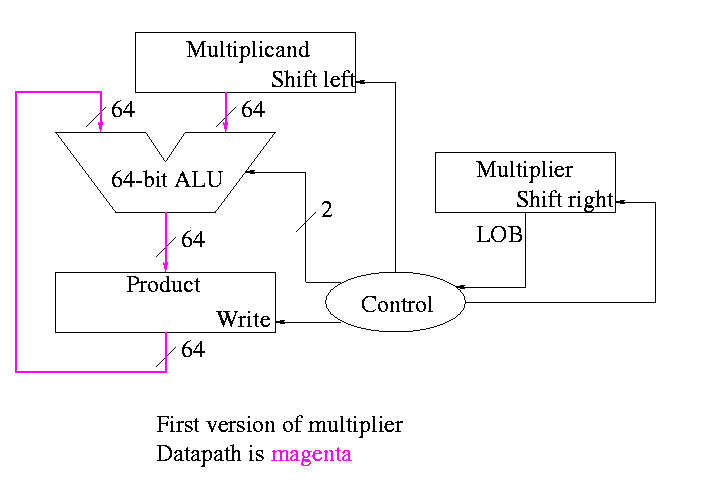
What about the control?

• Always give the ALU the ADD operation
• Always send a 1 to the multiplicand to shift left
• Always send a 1 to the multiplier to shift right
• Pretty boring so far but
  • Send a 1 to write line in product if and only if LOB multiplier is a 1
  • I.e. send LOB to write line
  • I.e. it really is pretty boring