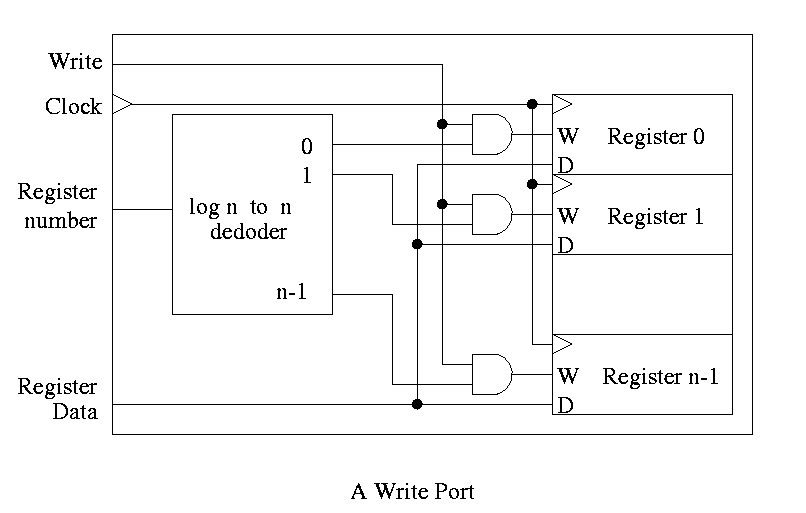
For writes use a decoder on register number to determine which register to write. Note that 3 errors in the book's figure were fixed

• decoder is log n to n
• decoder outputs numbered 0 to n-1 (NOT n)
• clock is needed

The idea is to gate the write line with the output of the decoder. In particular, we should perform a write to register r this cycle providing

• Recall that the inputs to a register are W, the write line, D the data to write (if the write line is asserted) and the clock.
• The clock to each register is simply the clock input to the register file.
• The data to each register is simply the write data to the register file.
• The write line to each register is unique
  • The register number is fed to a decoder.
  • The rth output of the decoder is asserted if r is the specified register.
  • Hence we wish to write register r if
    • The write line to the register file is asserted
    • The rth output of the decoder is asserted
    • Bingo! We just need an and gate.

Homework: 20

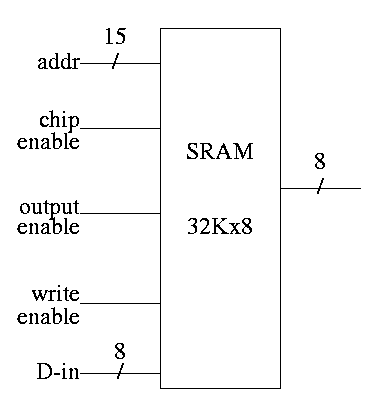
SRAMS and DRAMS

• External interface is below
• (Sadly) we will not look inside. Following is unofficial
  • Conceptually like a register file but can't use the implementation above for a large memory because there would be too many wires and the muxes would be too big.
  • Two stage decode
  • Tri-state buffers instead of mux for SRAM. Hence I was fibbing when I said that signals always have a 1 or 0. However, we will not use tristate logic (will use muxes the way we build them
  • DRAM latches whole row but outputs only one (or a few) column(s)
    • So can speed up access to elts in same Row
    • Merged DRAM + CPU a modern hot topic
• Error Correction (Omitted)

Note: There are other kinds of flip-flops T, J-K. Also one could learn about excitation tables for each. We will not cover this material (H&P doesn't either). If interested, see Mano

Counters

A counter counts (naturally). The counting is done in binary.

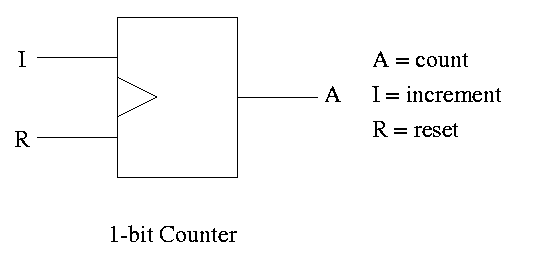
Let's look at the state transition diagram for A, the output of a 1-bit counter.

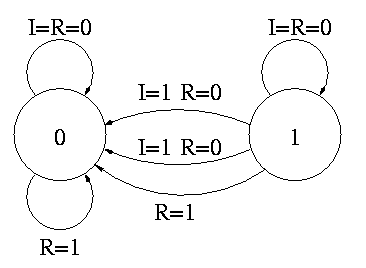
We need one flop and a combinatorial circuit.

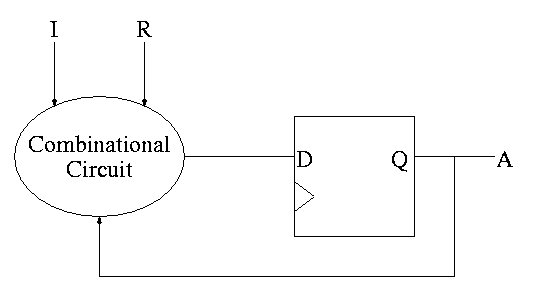
The flop producing A is often itself called A and the D input to this flop is called DA (really D sub A).

Current      Next ||
   A    I R   A   || DA <-- i.e. to what must I set DA
------------------++--      in order to
   0    0 0   0   || 0      get the desired Next A for
   1    0 0   1   || 1      the next cycle
   0    1 0   1   || 1
   1    1 0   0   || 0
   x    x 1   0   || 0

But this table (without Next A) is the truth table for the combinatorial circuit.

A I R  || DA
-------++--
0 0 0  || 0
1 0 0  || 1
0 1 0  || 1
1 1 0  || 0
x x 1  || 0

DA = R' (A XOR I)