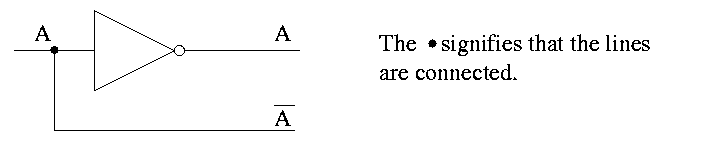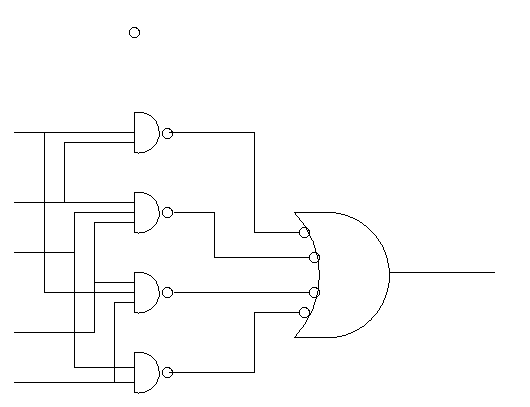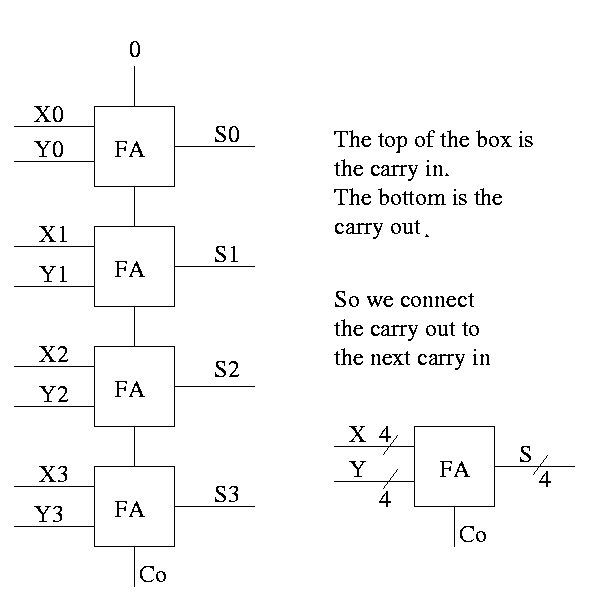Homework: B-12. Assume you have constant signals 1 and 0 as well.

Decoder

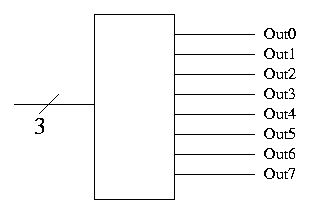
• Note the ``3'' with a slash, which signifies a three bit input. This notation represents three (1-bit) wires.
• Takes n signals in produces 2^n signals out
• View input as ``binary n'', the output has n'th bit set
• Implement on board with AND/OR

Encoder

• Reverse "function" of encoder
• Not defined for all inputs (exactly one must be 1)

Sneaky way to see that NAND is universal.

• First show that you can get NOT from NAND. Hence we can build inverters.
• Now imagine that you are asked to do a circuit for some function with N inputs. Assume you have only one output.
• Using inverters you can get 2N signals the N original and N complemented.
  
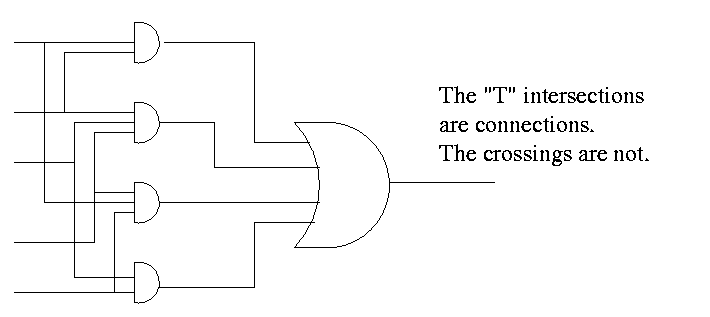
• Recall that the natural sum of products form is a bunch of ORs feeding into one AND.
  
• Naturally you can add pairs of bubbles since they ``cancel''
  
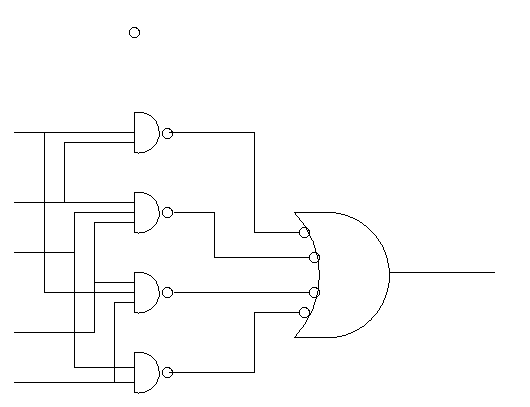
• But these are all NANDS!!

Half Adder

• Inputs X and Y
• Outputs S and Co (carry out)
• No CarryIn
• Draw TT

Homework: Draw logic diagram

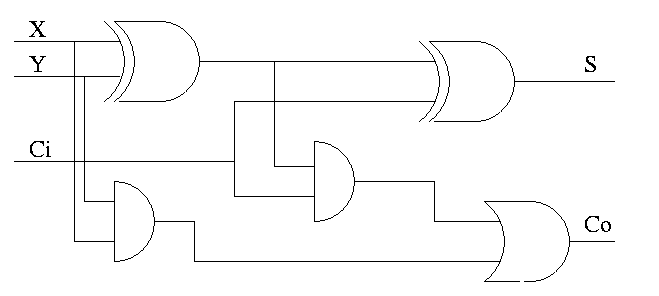
Full Adder

• Inputs X, Y and Ci
• Output S and Co
• S = #1s in X, Y, Ci is odd
• Co = #1s is at least 2

Homework:

• Draw TT (8 rows)
• show S = X XOR Y XOR Ci
• show Co = XY + (X XOR Y)Ci

How about 4 bit adder ?

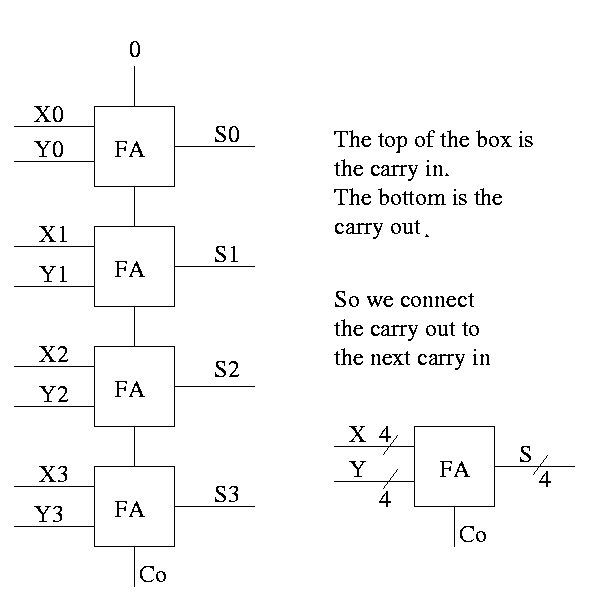
How about n bit adder ?

• Linear complexity
• Called ripple carry
• Faster methods exist