The first way we solved part E shows that any logic function can be written using just AND, OR, and NOT. Indeed, it is in a nice form. Called two levels of logic, i.e. it is a sum of products of just inputs and their compliments.

DeMorgan's laws:

• (A+B)' = A'B'
• (AB)' = A'+B'

You prove DM laws with TTs. Indeed that is ...

Homework: B.6 on page B-45

Do beginning of HW on the board.

With DM we can do quite a bit without resorting to TTs. For example one can show that the two expressions for E on example above (page B-6) are equal. Indeed that is

Homework: B.7 on page B-45

Do beginning of HW on board.

GATES

Gates implement basic logic functions: AND OR NOT XOR Equivalence

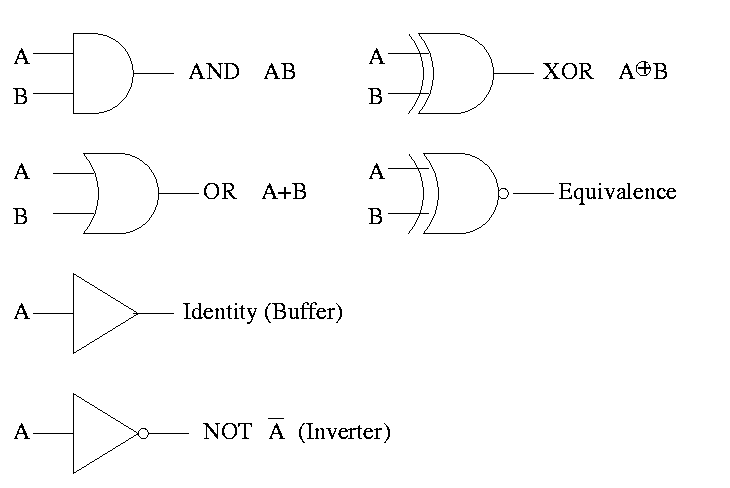
Show why the picture is equivalence, i.e (A XOR B)' is AB + A'B'

(A XOR B)' =
(A'B+AB')' = 
(A'B)' (AB')' = 
(A''+B') (A'+B'') = 
(A + B') (A' + B) = 
AA' + AB + B'A' + B'B = 
0   + AB + B'A' + 0 = 
AB + A'B'

Often omit the inverters and draw the little circles at the input or output of the other gates (AND OR). These little circles are sometimes called bubbles.

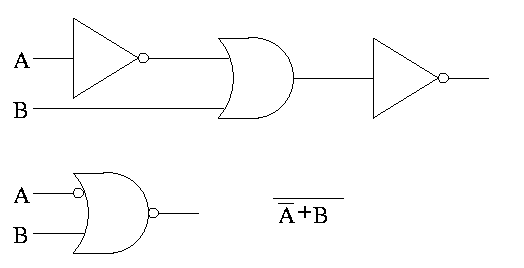
This explains why inverter is drawn as a buffer with a bubble.

Homework: B.2 on page B-45 (I previously did the first part of this homework).

Homework: Consider the Boolean function of 3 boolean vars (i.e. a three input function) that is true if and only if exactly 1 of the three variables is true. Draw the TT. Draw the logic diagram with AND OR NOT. Draw the logic diagram with AND OR and bubbles.

We have seen that any logic function can be constructed from AND OR NOT. So this triple is called universal.

Are there any pairs that are universal? Could it be that there is a single function that is universal? YES!

NOR (NOT OR) is true when OR is false. Do TT.

NAND (NOT AND) is true when AND is false. Do TT.

Draw two logic diagrams for each, one from definition and equivalent one with bubbles.

Theorem A 2-input NOR is universal and A 2-input NAND is universal.

Proof

We must show that you can get A', A+B, and AB using just a two input NOR.

• A' = A NOR A
• A+B = (A NOR B)' (we can use ' by above)
• AB = (A' OR B')'

Homework: Show that a 2-input NAND is universal.

Can draw NAND and NOR each two ways (because (AB)' = A' + B')

We have seen how to get a logic function from a TT. Indeed we can get one that is just two levels of logic. But it might not be the simplest possible. That is we may have more gates than necessary.

Trying to minimize the number of gates is NOT trivial. Mano covers this in detail. We will not cover it in this course. It is not in H&P. I actually like it but must admit that it takes a few lectures to cover well and it not used so much since it is algorithmic and is done automatically by CAD tools.

Minimization is not unique, i.e. there can be two or more minimal forms.

Given A'BC + ABC + ABC'
Combine first two to get BC + ABC'
Combine last two to get A'BC + AB

Sometimes when building a circuit, you don't care what the output is for certain input values. For example, that input combination is cannot occur. Another example occurs when, for this combination of input values, a later part of the circuit will ignore the output of this part. These are called don't care outputs situations. Making use of don't cares can reduce the number of gates needed.

Can also have don't care inputs when , for certain values of a subset of the inputs, the output is already determined and you don't have to look at the remaining inputs. We will see a case of this in the very next topic, multiplexors.

An aside on theory

Putting a circuit in disjunctive normal form (i.e. two levels of logic) means that every path from the input to the output goes through very few gates. In fact only two, an OR and an AND. Maybe we should say three since the AND can have a NOT (bubble). Theorticians call this number (2 or 3 in our case) the depth of the circuit. Se we see that every logic function can be implemented with small depth. But what about the width, i.e., the number of gates.

The news is bad. The parity function takes n inputs and gives TRUE if and only if the number of input TRUEs is odd. If the depth is fixed (say limited to 3), the number of gates needed for parity is exponential in n.

B.3 COMBINATIONAL LOGIC

Homework: Read B.3.

Generic Homework: Read sections in book corresponding to the lectures.

Multiplexor

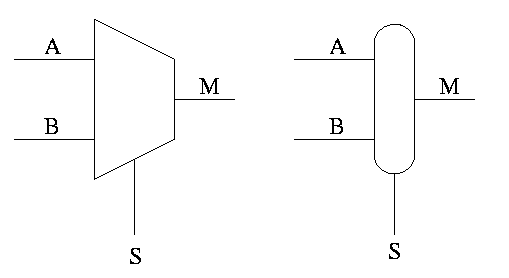
Often called a mux or a selector

Show equiv circuit with AND OR

Hardware if-then-else

    if S=0
        M=A
    else
        M=B
    endif

Can have 4 way mux (2 selector lines)

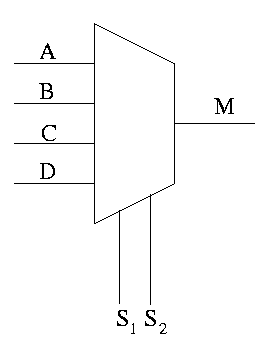
This is an if-then-elif-elif-else

   if S1=0 and S2=0
        M=A
    elif S1=0 and S2=1
        M=B
    elif S1=1 and S2=0
        M=C
    else -- S1=1 and S2=1
        M=D
    endif

Do a TT for 2 way mux. Redo it with don't care values.
Do a TT for 4 way mux with don't care values.