Administrivia

Web Pages

There is a web page for the course. You can find it from my home page.

• Can find these notes there. Let me know if you can't find it.
• They will be updated as bugs are found.
• Will also have each lecture available as a separate page. I will produce the page after the lecture is given. These individual pages might not get updated.

Textbook

Text is Hennessy and Patterson ``Computer Orgaiization and Design The Hardware/Software Interface''.

• Available in bookstore.
• The main body of the book assumes you know logic design.
• I do NOT make that assumption.
• We will start with appendix B, which is logic design review.
• A more extensive treatment of logic design is M. Morris Mano ``Computer System Architecture'', Prentice Hall.
• We will not need as much as mano covers and it is not a cheap book so I am not requiring you to get it. I will have it put into the library.
• My treatment will follow H&P not mano.
• Several of the figures from the text are available from the web and have been incorporated in these notes. The figures are for educational purposes only. The following copyright notice applies.
  ``All figures from Computer Organization and Design: The Hardware/Software Approach, Second Edition, by David Patterson and John Hennessy, are copyrighted material (COPYRIGHT 1998 MORGAN KAUFMANN PUBLISHERS, INC. ALL RIGHTS RESERVED). Figures may be reproduced only for classroom or personal educational use in conjunction with the book and only when the above copyright line is included. They may not be otherwise reproduced, distributed, or incorporated into other works without the prior written consent of the publisher.''

Homeworks and Labs

I make a distinction between homework and labs.

Labs are

• Required
• Due several lectures later (date given on assignment)
• Graded and form part of your final grade
• Penalized for lateness

• Optional
• Due beginning of Next lecture
• Not accepted late
• Mostly from the book
• Collected and returned
• Can help, but not hurt, your grade

Upper left board for assignments and announcements.

Appendix B: Logic Design

Homework: Read B1

B.2: Gates, Truth Tables and Logic Equations

Homework: Read B2 Digital ==> Discrete

Primarily (but NOT exclusively) binary at the hardware level

Use only two voltages -- high and low

• This hides a great deal of engineering
• Must make sure not to sample the signal when not in one of these two states.
• Sometimes it is just a matter of waiting long enough (determines the clock rate i.e. how many megahertz)
• Other times it is worse and you must avoid glitches.
• Oscilloscope traces shown below
  • Vertical axis is voltage; horizontal axis is time.
  • Square wave--the ideal. How we think of circuits
  • Sine wave
  • Actual wave
    • Non-zero rise times and fall times
    • Overshoots and undershoots
    • Glitches

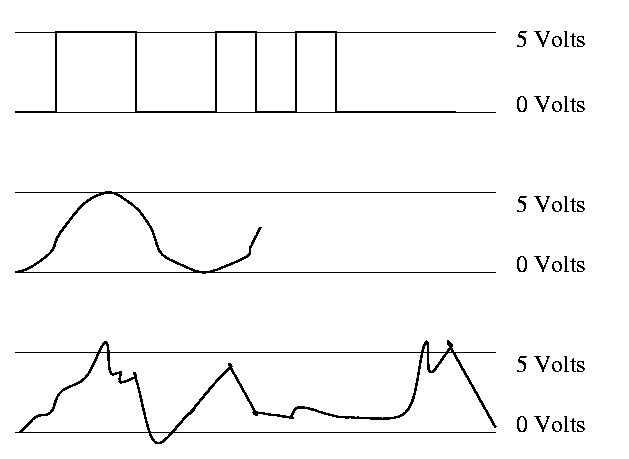
Since this is not an engineering course, we will ignore these issues and assume square waves.

In English digital (think digit, i.e. finger) => 10, but not in computers

Bit = Binary digIT

Instead of saying high voltage and low voltage, we say true and false or 1 and 0 or asserted and deasserted.

0 and 1 are called complements of each other.

A logic block can be thought of as a black box that takes signals in and produces signals out. There are two kinds of blocks

• Combinational (or combinatorial)
  • Does NOT have memory elements
  • Is simpler than circuits with memory since it is a function from the inputs to the outputs
• Sequential
  • Contains memory
  • The current value in the memory is called the state of the block.
  • The output depends on the input AND the state

We are doing combinational now. Will do sequential later (few lectures).

TRUTH TABLES

Since combinatorial logic has no memory, it is simply a function from its inputs to its outputs. A Truth Table has as columns all inputs and all outputs. It has one row for each possible set of input values and the output columns have the output for that input. Let's start with a really simple case a logic block with one input and one output.

There are two columns (1 + 1) and two rows (2**1).

In  Out
0   ?
1   ?

How many are there?

How many different truth tables are there for one in and one out?

Just 4: the constant functions 1 and 0, the identity, and an inverter (pictures in a few minutes). There were two `?'s in the above table each can be a 0 or 1 so 2**2 possibilities.

OK. Now how about two inputs and 1 output.

Three columns (2+1) and 4 rows (2**2).

In1 In2  Out
0   0    ?
0   1    ?
1   0    ?
1   1    ?

How many are there? It is just how many ways can you fill in the output entries. There are 4 output entries so answer is 2**4=16.

How about 2 in and 8 out?

• 10 cols
• 4 rows
• 2**(4*8)=4 billion possible

3 in and 8 out?

• 11 cols
• 8 rows
• 2**(8**8)=2**64 possible

n in and k out?

• n+k cols
• 2**n rows
• 2**([2**n]*k) possible

Gets big fast!

Boolean algebra

Certain logic functions (i.e. truth tables) are quite common and familiar.

We use a notation that looks like algebra to express logic functions and expressions involving them.

The notation is called Boolean algebra in honor of George Boole.

A Boolean value is a 1 or a 0.
A Boolean variable takes on Boolean values.
A Boolean function takes in boolean variables and produces boolean values.

1. The (inclusive) OR Boolean function of two variables. Draw its truth table. This is written + (e.g. X+Y where X and Y are Boolean variables) and often called the logical sum. (Three out of four output values in the truth table look right!)
   
   
2. AND. Draw TT. Called log product and written as a centered dot (like product in regular algebra). All four values look right.
   
   
3. NOT. Draw TT. This is a unary operator (One argument, not two like above; the two above are called binary). Written A with a bar over it (I will use ' instead of a bar as it is easier for my to type).
   
   
4. Exclusive OR (XOR). Written as + with circle around. True if exactly one input is true (i.e. true XOR true = false). Draw TT.

Homework: Consider the Boolean function of 3 boolean vars that is true if and only if exactly 1 of the three variables is true. Draw the TT.

Some manipulation laws. Remember this is Boolean ALGEBRA.

Identity:

• A+0 = 0+A = A
• A.1 = 1.A = A
• (using . for and)

Inverse:

• A+A' = A'+A = 1
• A.A' = A'.A = 0
• (using ' for not)

Both + and . are commutative so don't need as much as I wrote

The name inverse law is somewhat funny since you Add the inverse and get the identity for Product or Multiply by the inverse and get the identity for Sum.

Associative:

• A+(B+C) = (A+B)+C
• A.(B.C)=(A.B).C

Due to associative law we can write A.B.C since either order of evaluation gives the same answer.

Often elide the . so the product associative law is A(BC)=(AB)C.

Distributive:

• A(B+C)=AB+AC
• A+(BC)=(A+B)(A+C)
• Note that BOTH distributive laws hold UNLIKE ordinary arithmetic.

How does one prove these laws??

• Simple (but long) write the TTs for each and see that the outputs are the same.
• Do the first dist laws on the board.

Homework: Do the second distributive law.

Let's do (on the board) the examples on pages B-5 and B-6. Consider a logic function with three inputs A, B, and C; and three outputs D, E, and F defined as follows: D is true if at least one input is true, E if exactly two are true, and F if all three are true. (Note that by if we mean if and only if.

Draw the truth table.

Show the logic equations

• For E first use the obvious method of writing one condition for each 1-value in the E column i.e.
  (A'BC) + (AB'C) + (ABC')
• Observe that E is true if two (but not three) inputs are true, i.e.,
  (AB+AC+BC) (ABC)' (using . higher precedence than +)