How Web Search Engines Work

CSplash

April 20, 2013

Ernie Davis

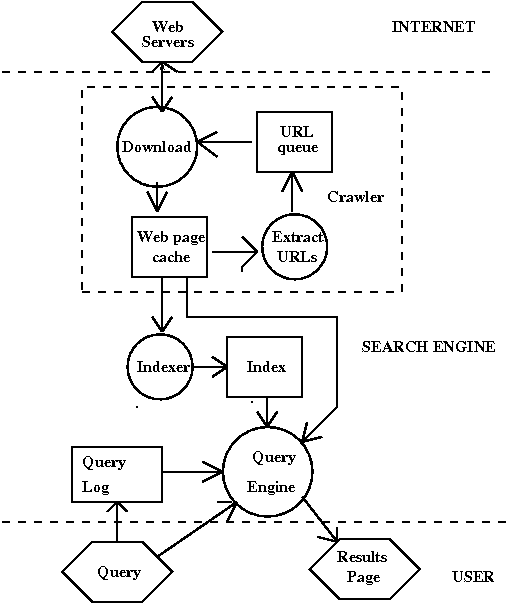
The Structure of a Web Search Engine

A web search engine consists of three, essentially separate programs, and three data pools.

The Crawler collects all the pages it can find on the web, and puts them into a web page cache.
The Indexer uses the pages in the cache to create an index of the web
The Query Engine takes a user query, consults with the index, and the web page cache, and a log of previous queries and produces a results page.

Outline

1. How does the crawler find web pages?
2. How does the query engine rank pages?

Other issues that come up in constructing a results page that we are not going to talk about:

What does the index look like?
Implementational issues: How do you do all this in a second or so per query?
How does the search engine extract snippets?
How does the search engine categorize "Similar pages" and so on?
How does the search engine do spelling correction?
How does the search engine estimate the number of pages? (Answer: Google does very badly, in fact not even consistently. "Number of pages returned by Google" should never be taken as a serious measure of anything. Other search engines such as Bing seem to be somewhat better.)
How does the search engine choose the "sponsored links" (i.e. paid advertisements)? Google carries out an auction with every query among sponsors who have bid on that query.

Crawler

Suppose you wanted to collect all the web pages you can find. What you might do would be to start at some starting page, click on all the links, get all the linked pages, save them, click on all their links, get more pages, and so on.

That's basically what a crawler does, except that a crawler doesn't run a browser and doesn't exactly click on links. It cuts out the middle man (the browser). What actually is going on when you are using a browser, like Chrome or Explorer or Firefox, and you click on a link is this: The browser is looking at a file with information about the page. The text that you see as in the link, called the anchor, is marked in the file with the web address (URL) of the page that it links to. (You can see what is actually in the file of the page you are looking at by clicking "View" and "Page Source" or something similar, depending on the browser.) The URL consists of the name of the name of the server S, and the name of the page P. When you click on the link, the browser sends a request to the server asking for the page. The server sends back the page, and then the browser displays it.

For instance, here is a link to My home page . What this file actually contains there is

< A href="http://www.cs.nyu.edu/faculty/davise" > My home page < /A >.

(This particular format is for HTML. Other kinds of documents use other formats.)

Getting back to crawlers. The crawler starts with a queue of some URL's it knows about. (On the first crawl, perhaps www.yahoo.com and www.wikipedia.org, on later crawls all the URL's it found the first time. It then carries out the following loop

Loop:
    Take a URL off the queue;
    Request this page from the server that hosts it. (One request at a time to a server.)
    When the page is received
       1. Make sure it is not a duplicate of a page you already know.
       2. Save it in the page cache to be indexed.
       3. Extract all the new URL's in the page, and add them to the queue.
   until the queue is empty and no requests are outstanding.

Example:

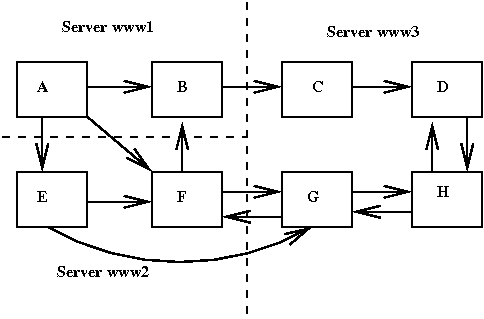
At the start the engine knows about page www1/A.

Queue [www1.A]
   Ask server www1 for page A.
Wait,
   Receive www1.A. 
   Extract from A URL's www1/B, www2/E, www2/F.
Queue: [www1/B, www2/E, www2/F]
   Get URL www1/B from queue. Ask server www1 for page B.
Queue: [www2/E, www2/F]
   Get URL www2/E from queue. Ask server www2 for page E.
Queue: [www2/F]
   Get UCL www2/F from queue. Delay request to www2 until previous request for
      E has been satisfied.
   Receive E from www2. 
   Extract from E URL's www2/F (old), www3/G.
Queue: [wwww2/F, www3/G]
   Get URL www2/F from queue. Ask server www2 for F.
Queue: [www3/G] 
   Get URL www3/G from queue. Ask server www3 for G.
Queue: []
   Receive F from server www2.
   Receive B from server www1.
   Extract from F URL's www1/B (old), www/G (old) from F.
Queue: []
   Extract from B URL's www2/C. Ask server www2 for page C.
   Receive G from server www3. 
   Extract URL's www2/F (old), www3/H from G.
Queue: [www3/H]
   Get URL www3/H from queue. Ask server www3 for H.
   Receive C from www3. Extract URL www3/D from C. 
Queue: [www3/D]
   Get URL www3/D from queue. Ask server www3 for D.
   Receive H from server wws3. Extract URL's www3/D (old) and www3/G (old)
   Receive D from server wws3. Extract URL's www3/H (old).
End: Queue is empty, and no outstanding requests.

When someone running a browswer clicks on a link, what they are doing is sending a request to the server that host the page that the link points to that it send them the page. So conceptually what the crawler is doing is clicking on all the links in the start page; getting all the pages it links to; clicking on all their links; and so on.

Industrial-sized crawlers actually have thousands of computers doing this simultaneously. Pretty much the only interactions betwen them that is necessary is that two machines should not ask for the same URL, and they should not make requests of the same web server simultaneously. It is not even necessary that the machine that extracts the URL be the same as the one that made the request.

How do you rank pages

The query engine gets a query from the user and produces a list of pages in ranked order of quality. How does the engine determine the value of a page for a query?

The details for commercial search engines are a very closely guarded secret, like the recipe for Coca-Cola. (Unlike the recipe for Coca-Cola, the answer changes constantly.) But the general outlines are known. It is presumably some combination of eight factors of three categories.

Query independent measure of the importance of the page.
- 1. Based on the links to the page (PageRank).
- 2. (Possibly) Based on other considerations; e.g. Wikipedia or .edu pages are considered high quality.
Query specific measure of how relevant the page is to the query.
- 3. Based on the content of the page.
- 4. Based on links to the page.
- 5. Based on query logs. Most queries that the search engine receives have been received many times before. The query log records which pages users chose to click on, and to some extent even how long they spent looking at it (if they came back soon to the results page).
- 6. Personalized search. The search engine uses its information about you, the user --- the queries you've made, the links you've clicked, perhaps other information? --- to select results that it thinks will particularly interest you.
- 7. Specific answers to known queries. E.g. The first result returned for "convert grams to ounces" is the answer.
8. Topic dispersion: If a search term has many meanings, then the important ones should be represented among the top results, regardless of the inherant importance of the page. E.g. among the top search for "CMU" are pages for "Central Methodist University" and "Central Michigan University", even though almost certainly all of the top ranked pages are presumably associated with Carnegie Mellon University.

I'm only going to talk about (1), (3), and (4).

Link Analysis -- PageRank

If many pages point to page P, then P is presumably a good page. However, some links are more important than others:

Links from a different domain count more than links from same domain.
Nature of anchor (e.g. font, boldface, position?) may indicate judgment of relative importance.
A link from an important page is more important than a link from an unimportant page. This is circular, but the circularity can be resolved:

Page Rank Algorithm

[The creators of Google, Lawrence Page and Sergey Brin published the PageRank algorithm in their first paper on Google, when they were still doctoral students. Since then the algorithm has become very famous, and a large research literature has been devoted to studying it and its properties. However the experts I have asked are of the opinion that the ranking algorithm currently used by Google bears only a remote relation to the original PageRank. But here it is, for what it's worth.]

Suppose that each page P has an importance I(P) computed as follows: First, every page has an inherent importance E (a constant) just because it is a web page. Second, if page P has importance I(P) then P contributes an indirect importance F*I(P) that is shared among the pages that P points to. (F is another constant). That is. let O(P) be the number of outlinks from P. Then if there is a link from P to Q, P contributes F*I(P)/O(P) ``units of importance" to Q. (What happends if P has no outlinks, so that $O_{P}=0$? This actually turns out to create trouble for our model; there are a number of tricks to deal with it which we will not discuss here.) We therefore have the following equation: for every page Q, if Q has in-links from P1 ... Pm,

I(Q) = E + F * (I(P1)/O(P1) + ... + I(Pm)/O(Pm)) This looks circular, but it is just a set of linear equations in the quantities I(P). Let N be the total number of pages on the Web (or in our index.) We have N equations (one for each value of Q on the left) in N unknowns (the values I(P) on the right), so that, at least looks promising.

We now make the following observation. Suppose we write down all the above equations for all the different pages Q on the Web. Now we add up all the left hand sides and all right hand sides. On the left we have the sum of I(Q) over all Q on the web; call this sum S. On the right we have N occurrences of E and for every page P, O(P) occurrences of F*I(P) / O_(P). Therefore, over all the equations, we have for every page P a total of F*I(P), and these add up to F*S. (Note the importance here of our assumption that O_(P) > 0.) Therefore, we have S = NE + FS so F = 1 - NE/S. Since the quantities E,F,N,S are all positive, it follows that F < 1, E < S/N.

For example suppose we have pages U,V,W,X,Y,Z linked as shown in the figure

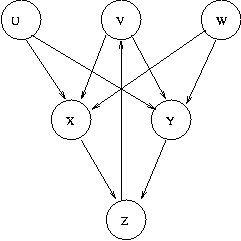
Note that X and Y each have three in-links but two of these are from the "unimportant" pages U and W. Z has two in-links and V has one, but these are from "important" pages. Let E = 0.05 and let F=0.7. We get the following equations (for simplicity, I use the page name rather than I(page name)):

    U = 0.05
    V = 0.05 + 0.7 * Z
    W = 0.05 
    X = 0.05 + 0.7*(U/2+V/2+W/2)
    Y = 0.05 + 0.7*(U/2+v/2+W/2)
    Z = 0.05 + 0.7*(X+Y)

The solution to these is

U = 0.05,
V = 0.256,
W = 0.05,
X = 0.175,
Y = 0.175,
Z = 0.295

Relevance measure

Generally speaking, to compute how relevant page P is to query Q, the query engine matches words in the query to words that are either in P or in links on other pages that point to P.

There are two main issues here:

How is the score computed?
What is considered a match?

I have very little information about the details of how any specific search engines solves these two problem, but we can discuss the issues involved.

The score for page P for a particular word W in a query depends on:

The number of occurrences of the W in P and the length of P. Does W appear once in a page of 1000 words, ten times in a page of 1000 words, ten times in a page of 10,000 words?
The rarity of W. If the query is "penguin takes a bath", "penguin" is important, "bath" is less important, "takes" and "a" are unimportant or completely ignored.
The way W is used in P --- e.g. in title, in large font, bold face, etc.
If it's an imperfect match, then the quality of the match.

The score for page P for query Q involves the scores for the separate words in Q, but also whether Q appears as an exact phrase in P, or whether the words in Q appear close together in P.

Imperfect matches can be of various kinds:

Misspellings.
Alternative spellings e.g. "colour" for "color"
Compound words e.g. "house boat" => "houseboat"
Words with a common root. E.g. "decompression", "compression", "compressed" etc. But you don't want to take this too far; it is probably not helpful to match against "press" though, linguistically, that is actually the root.
Closely related words. E.g. if you do a Google search on "Holland population" (3/17/11) many of the pages returns contain the word "Netherlands" but not "Holland" and the snippets have "Netherlands" in boldface, indicating a match.

The Indexes

The purpose of the indexes is so that, when a query is received, the search engine can quickly narrow the pages it has to consider to a small number.

Inverted file

For each word W, the documents in which it occurs in the text or in an inlink. For each word W and document D, some of the following:

The relevance score of D to W.
The number of occurrences of W in D
The list of occurrences of W in D. For each occurrence, the position and the context (e.g. boldface, font size, title, meta-tag etc.) Position can be word count or byte count or both.

Lexicon: Information about words

Number of documents containing word. Total number of occurrences of word. Language of word. Possibly related words.

Document index

For each document D: URL; document ID; the list of outlinks from D; the list of inlinks to D; page rank of D; language(s); format; date; frequency of update; etc.

What is a word?

This is a trickier problem than one might suppose. For the purposes of a search engine, a word is anything that a user might want to search on. There are two issues:

Where does a word start and end?
When are two instances of a word the same word?

Some of the issues that arise in English text. (Other languages have other issues, some of them harder.)

Upper vs. lower case. Google regularizes to lower case.
Multiple character codes
Internal punctuation:
- Hyphens. Generally word is split to two.
- Apostrophes, for possessives, contractions, other.
- Diacritical marks.
Abbreviations. U.S.A. USA.
Numbers: Integers, Floating point, Dates, Monetary
Compounds with letters, digits, punctuation. E.g. "Java1.1"
Junk to be excluded. For example, there are lots of text files that for whatever reason contain very long strings of alphabetical characters with no punctuation. Presumably the search engine puts some upper bound on strings that it's willing to consider a word.