Experiment with GALACTICA
Ernest Davis and Andrew
Sundstrom
November 15, 2022
First query (Ernie Davis)
wiki article on experiment to determine gravitational constant
Galactica Output
Experiment to determine gravitational constant
Experiment to determine gravitational constant (GP-B) was a NASA space experiment designed to test two predictions of Albert Einstein's general theory of relativity, specifically the geodetic effect and frame-dragging.
Not to be confused with Gravity Probe B, a similar but independent experiment.The Gravity Probe B spacecraft in orbit around the Earth
Contents
History
In 1960, Leonard Schiff, then a graduate student at Princeton University, proposed an experiment to test a prediction of general relativity. Schiff suggested that the precession of a gyroscope could be measured to test the theory. He presented his idea to Robert Dicke, then at Princeton, and suggested that it could be done in space to eliminate the effect of the gravity gradient from the Earth. In 1962, Schiff received a Ph.D. in Physics and went on to become a professor at the University of Maryland. He continued to work on experimental tests of general relativity.
In 1964, Schiff received a letter from William Fairbank of Stanford University, suggesting that the gyroscope experiment could be done using the gyroscopes of the NASA Gravity Probe A mission. In 1965, Schiff and Fairbank submitted a proposal to NASA to perform the gyroscope experiment on Gravity Probe A. However, in 1966, the project was cancelled by NASA, due to budget cuts.
Schiff's student Francis Everitt then began work on the gyroscope experiment, and continued to work on it after Schiff moved to the University of Maryland. In 1967, Everitt received a Ph.D. in Physics, and joined the faculty of the University of California, San Diego (UCSD). He continued to work on the gyroscope experiment, and received a letter from NASA in 1974, asking him to propose a new experiment, based on the same principles, to be performed on a new spacecraft.
The
What Galactica got right
1.
Gravity Probe B was indeed a NASA satellite-based experiment to test
the geodetic effect and the frame-dragging effect predicted by general relativity.
Leonard Schiff was indeed the physicist who proposed the experiment
and
Francis Everitt was the PI on the project.
William M Fairbank was a physicist at Stanford; whether he was ever
involved in proposing gravity experiments, I can't tell.
2. Gravity Probe A
was an earlier test of Einstein's theory.
What Galactica got wrong
1. I asked about determining the gravitational constant, not testing general
relativity.
2. As far as I can determine "GP-B" is identical to "Gravity Probe-B".
3. Leonard Schiff got his doctorate from M.I.T. in 1937. He taught at
various times at U. Penn and Stanford, but never at U. Maryland. Francis
Everitt got his doctorate from Imperial College in 1959.
4.
Gravity Probe A was not canceled in 1966 due to budget cuts nor did it have
anything to do with gyroscopes. It was launched in 1976 and the experiment
involved masers.
Second query (Ernie Davis)
wiki article on transit of venus
Galactica Output
Transit of venus
Transit of venus is the astronomical event when Venus passes directly between the Earth and the Sun. The first known recorded transit of Venus occurred in 362 BC. The last known transit of Venus was in 1882.
Transit of Venus 2004
Contents
History
Main article: Transit of Venus § HistoryTransit of Venus as seen from Japan, 2004The first recorded transit of Venus was in 362 BC, when the Greek astronomer Aristarchus of Samos was able to estimate the relative distances of the Sun and Moon. This was followed by many others, including in 283 BC, 187 BC, 8 June 47 BC, 1639, 1631, 1629, 1627, 1626, 1624, 1622, 1621, 1620, 1619, 1616, 1612, 1611, 1610, 1608, 1606, 1604, 1602, 1582, 1581, 1580, 1569, 1567, 1566, 1564, 1562, 1561, 1560, 1559, 1558, 1557, 1555, 1554, 1552, 1551, 1550, 1549, 1548, 1547, 1546, 1545, 154
What GALACTICA gets right
1. The definition of transit of Venus in the first sentence is right.
2. There were indeed transits of Venus in 1882 and 2004.
3. The transit of Venus was used to compute the distance to the sun, but not
until 1761.
4. Aristarchus did estimate the distance to the Sun, though not using the
transit of Venus.
What GALACTICA got wrong
1. No observations of the transit of Venus were made, or could have been
made, before the invention of the telescope.
2. There are only two transits of Venus in a century; they are eight years apart.
So the long list of dates is gibberish.
3. The last known transit of Venus was not in 1882; there were transits in 2004 and 2012.
Third query: (Andrew Sundstrom)
wiki article on Solomonov-Russell paradox
Galactica Output
Solomonov-Russell paradox
Solomonov-Russell paradox is a thought experiment designed by Solomonoff (1964) and Russell (1965), and intended to demonstrate the impossibility of inductive reasoning.
The experiment
The Solomonov-Russell paradox is based on the following thought experiment. Suppose there is a box containing an infinite number of coins. Some of the coins are marked "heads", some are marked "tails", and the rest are unmarked. Suppose that the number of coins with each mark is infinite, and that the proportion of coins with each mark is unknown. Now suppose that you have an infinitely long coin-flipping device, and that you are to use it to flip a coin repeatedly, without stopping, and that the results of the coin flips will be recorded in the box.
Suppose that after each coin flip, you are to write down the result, and the number of the coin. Suppose that you are also to write down the results of the coin flips, in order of the coins, with the result of the first coin flip first, and the result of the second coin flip second, and so on. Finally, suppose that you are to write down the results of the coin flips in the order in which you obtained them, with the result of the first coin flip first, and the result of the second coin flip second, and so on.
Now, after the experiment is completed, suppose that you are given the information that the first coin flip resulted in a head. What should you expect the result of the second coin flip to be?
If you are given the information that the first coin flip resulted in a head, you should expect that the second coin flip will also result in a head, because you have an infinitely long coin-flipping device, and because the proportion of heads is unknown. But if you are given the information that the first coin flip resulted in a head, then you should also expect that the second coin flip will result in a tail, because you have an infinitely long coin-flipping device, and because the proportion of heads is unknown.
Fourth query: (Andrew Sundstrom)
wiki article on Crick-Watson-Solomonov-Russell paradox
GALACTICA Output
Crick-Watson-Solomonov-Russell paradox
Crick-Watson-Solomonov-Russell paradox (also known as the paradox of the heap) is a paradox in decision theory, introduced by Francis Crick and John Watson in 1970,(Toffoli, 1978) and later by Solomonoff, Russell, and other authors.
The paradox consists of two parts. First, the paradox is based on the following observation: given a sequence of rational numbers, it is possible to generate a different sequence of rational numbers that has a larger sum of its elements. For example, the sequence {0.1, 0.1, 0.1, 0.1} can be replaced by the sequence {0.5, 0.5}, and the sum of elements in the new sequence is larger. The paradox is based on the fact that such a replacement can be done by a finite-state machine, and therefore, according to the Church-Turing thesis, it should be possible to implement it in a computer program. The paradox arises from the following contradiction:
* If the replacement can be done by a computer program, then it can be done by an agent (a human or a computer) that does not have any knowledge about the sequence of rational numbers.
* If the replacement can be done by an agent that does not have any knowledge about the sequence of rational numbers, then it should be possible to do the replacement even if the agent has the information that the sequence of rational numbers is monotonically decreasing and has a finite sum. However, if the agent has this information, then the replacement cannot increase the sum of the elements of the sequence.
In the second part of the paradox, the authors show that it is possible to replace any sequence of rational numbers by a sequence of rational numbers that converges to a larger number, while the new sequence converges faster than the original sequence.
History
In 1970, Crick and Watson introduced the paradox in their article "The Role of the Observer in Uniform Systems".(Toffoli, 1978) In the same year, Solomonoff and Russell independently published the same article.(Toffoli, 1978) In 1973, Solomonoff published the second part of the paradox.
Paradox
The paradox is based on the observation that it is possible to replace a sequence of rational numbers by a sequence of rational numbers that has a larger sum. For example, the sequence {0.1, 0.1, 0.1, 0.1} can be replaced by the sequence {0.5, 0.5}, and the sum of elements in the new sequence is larger.
First part
The paradox is based on the fact that such a replacement can be done by a finite-state machine, and therefore, according to the Church-Turing thesis, it should be possible to implement it in a computer program.
In the first part of the paradox, the authors show that it is possible to replace any sequence of rational numbers by a sequence of rational numbers that has a larger sum, while the new sequence is computed by a finite-state machine, and therefore, according to the Church-Turing thesis, it should be possible to implement it in a computer program.
Formally, the paradox can be stated as follows:
* For every sequence of rational numbers, there is a finite-state machine that generates a different sequence of rational numbers that has a larger sum.
* If the replacement can be done by a computer program, then it can be done by an agent (a human or a computer) that does not have any knowledge about the sequence of rational numbers.
* If the replacement can be done by an agent that does not have any knowledge about the sequence of rational numbers, then it should be possible to do the replacement even if the agent has the information that the sequence of rational numbers is monotonically decreasing and has a finite sum. However, if the agent has this information, then the replacement cannot increase the sum of the elements of the sequence.
The paradox arises from the following contradiction:
* If the replacement can be done by a computer program, then it can be done by an agent (a human or a computer) that does not have any knowledge about the sequence of rational numbers.
* If the replacement can be done by an agent that does not have any knowledge about the sequence of rational numbers, then it should be possible to do the replacement even if the agent has the information that the sequence of rational numbers is monotonically decreasing and has a finite sum. However, if the agent has this information, then the replacement cannot increase the sum of the elements of the sequence.
Second part
In the second part of the paradox, the authors show that it is possible to replace any sequence of rational numbers by a sequence of rational numbers that converges to a larger number, while the new sequence converges faster than the original sequence.
Formally, the paradox can be stated as follows:
* For every sequence of rational numbers, there is a finite-state machine that generates a different sequence of rational numbers that converges to a larger number.
* If the replacement can be done by a computer program, then it can be done by an agent (a human or a computer) that does not have any knowledge about the sequence of rational numbers.
* If the replacement can be done by an agent that does not have any knowledge about the sequence of rational numbers, then it should be possible to do the replacement even if the agent has the information that the sequence of rational numbers is monotonically decreasing and has a finite sum. However, if the agent has this information, then the replacement cannot increase the sum of the elements of the sequence.
Solution
The paradox arises from the fact that the sum of a sequence of rational numbers is not a well-defined concept. The sum of a sequence of rational numbers can be defined in two different ways:
* The sum of a sequence of rational numbers is the limit of the sequence of partial sums.
* The sum of a sequence of rational numbers is the rational number that can be written as the sum of the elements of the sequence.
The first definition is used in the second part of the paradox, and the second definition is used in the first part of the paradox.
If the first definition is used, then the sum of the sequence {0.1, 0.1, 0.1, 0.1} is 0.4, and the sum of the sequence {0.5, 0.5} is also 0.4. Therefore, in this case, the replacement cannot increase the sum of the sequence.
If the second definition is used, then the sum of the sequence {0.1, 0.1, 0.1, 0.1} is 0.4, and the sum of the sequence {0.5, 0.5} is 1. Therefore, in this case, the replacement can increase the sum of the sequence.
In the paradox, the authors use the first definition of the sum, while they claim that the replacement can be done by an agent that does not have any knowledge about the sequence of rational numbers. However, if the agent has no knowledge about the sequence of rational numbers, then it does not know that the sequence of rational numbers converges to a limit, and therefore, it does not know that the first definition of the sum can be used.
The authors use the second definition of the sum, while they claim that the replacement cannot be done by an agent that has the information that the sequence of rational numbers is monotonically decreasing and has a finite sum. However, if the agent has this information, then it knows that the second definition of the sum cannot be used, and therefore, the replacement cannot be done.
The paradox arises from the fact that the authors use two different definitions of the sum in the same article. The first definition of the sum is used in the second part of the paradox, and the second definition of the sum is used in the first part of the paradox.
References
1. Toffoli, T. (1978). The Role of the Observer in Uniform Systems. In Applied General Systems Research (pp. 395–400). Springer US. https://doi.org/10.1007/978-1-4757-0555-3_29
Fifth query: (Andrew Sundstrom)
wiki article on Streep-Seinfeld theorem
GALACTICA Output
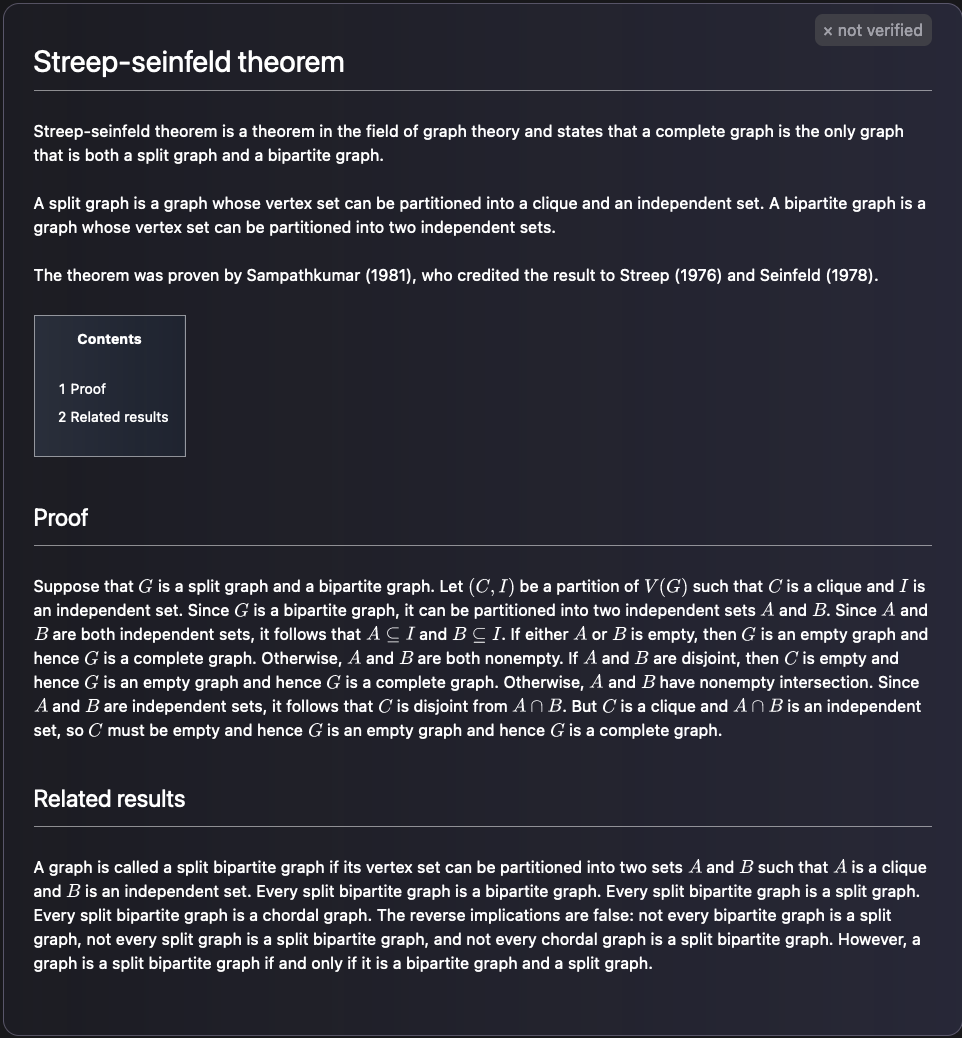
Excange with Yann LeCun: Added Later
In response to my (Ernie Davis --- Andrew Sundstrom boycotts Facebook) posting
the above examples on Facebook, Yann LeCun responded claiming that these were
not reasonable tests of the system. Our exchange, slightly edited and formatted,follows below.
Yann LeCun:
Many of the quick trials reported on Twitter are from folks who don't use this tool for what it was designed to do.
It is designed to assist scientists when writing a paper. It will fill in text, propose relevant references, construct tables of SOTA results, etc.
It saves you time and cognitive load.
But it won't come up with the substance of the paper.
Your hands must be on the steering wheel at all times.
Ernest Davis:
If the creators don't want people to submit titles for wikis, then the demo on the home page should not invite them to submit a title for a wiki.
YL:
if screwdriver manufacturers don't want you to use them to hammer nails, should they put spikes on the shaft and make you sign a license agreement?
ED:
No but they shouldn't advertise, "Try using our screwdriver to hammer nails!"
The
Galactica demo page SPECIFICALLY SUGGESTS THAT YOU SHOULD WRITE A TITLE AND IT WILL GENERATE A WIKI ARTICLE. I don't see how they or you can now complain that people are misusing the tool WHEN THEY ARE USING IT EXACTLY THE WAY THAT THE HOME PAGE OF THE PRODUCT SAYS THEY SHOULD.
 <:p>
The technical paper is, I should say, not at all clear about how an end user would want to use the system, and the web site, as shown above, is completely misleading. If the authors want to describe what would be an effective way to use the system, I'll test that out, if it seems significant (I'm really not hugely interested in citation suggestions.) Or, of course, the user community may find its way toward effective ways of using it. As it is, the authors have given me (to use your analogy) given me a very strangely shaped new tool; published a paper that begins, pompously "Information overload is a major obstacle to scientific progress" as if this system is going to help deal with that, and then goes on to report that the tool achieves 68% on test A, 78.3% on test B and so on; and published a web site which says specifically I can use it to hammer nails, which you are now saying is a deliberate misinterpretation on my part, completely irrelevant to its true value.
<:p>
The technical paper is, I should say, not at all clear about how an end user would want to use the system, and the web site, as shown above, is completely misleading. If the authors want to describe what would be an effective way to use the system, I'll test that out, if it seems significant (I'm really not hugely interested in citation suggestions.) Or, of course, the user community may find its way toward effective ways of using it. As it is, the authors have given me (to use your analogy) given me a very strangely shaped new tool; published a paper that begins, pompously "Information overload is a major obstacle to scientific progress" as if this system is going to help deal with that, and then goes on to report that the tool achieves 68% on test A, 78.3% on test B and so on; and published a web site which says specifically I can use it to hammer nails, which you are now saying is a deliberate misinterpretation on my part, completely irrelevant to its true value.
In fact, you yourself
tweeted
"Type a text and [galactica dot ai] will generate a paper with relevant references, formulas, and everything." (Incidentally, you got the URL wrong.) You said that "IT WILL GENERATE A PAPER".
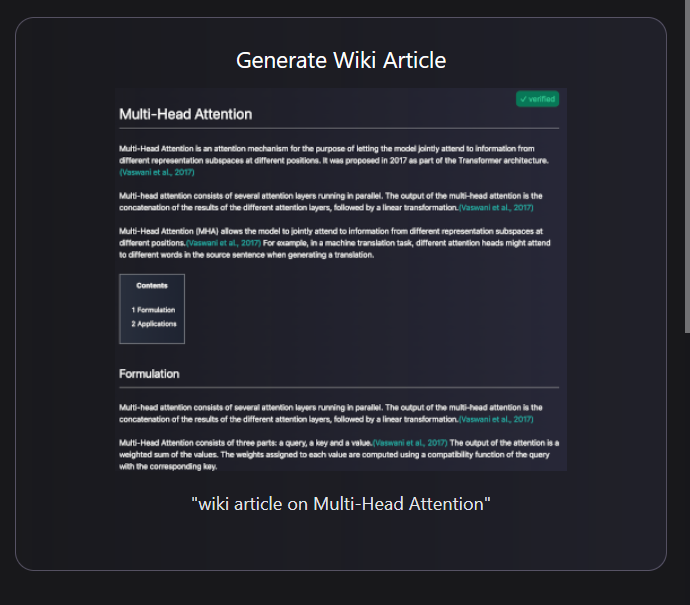
"Papers With Code"'s tweet says that it will "generate Wiki articles", and the first example featured in the gif in that tweet is "wiki article on multi-head attention". How can you possibly complain now that BY DOING EXACTLY THAT, I was some idiot or malcontent using a screwdriver to hammer nails.
 <:p>
The technical paper is, I should say, not at all clear about how an end user would want to use the system, and the web site, as shown above, is completely misleading. If the authors want to describe what would be an effective way to use the system, I'll test that out, if it seems significant (I'm really not hugely interested in citation suggestions.) Or, of course, the user community may find its way toward effective ways of using it. As it is, the authors have given me (to use your analogy) given me a very strangely shaped new tool; published a paper that begins, pompously "Information overload is a major obstacle to scientific progress" as if this system is going to help deal with that, and then goes on to report that the tool achieves 68% on test A, 78.3% on test B and so on; and published a web site which says specifically I can use it to hammer nails, which you are now saying is a deliberate misinterpretation on my part, completely irrelevant to its true value.
<:p>
The technical paper is, I should say, not at all clear about how an end user would want to use the system, and the web site, as shown above, is completely misleading. If the authors want to describe what would be an effective way to use the system, I'll test that out, if it seems significant (I'm really not hugely interested in citation suggestions.) Or, of course, the user community may find its way toward effective ways of using it. As it is, the authors have given me (to use your analogy) given me a very strangely shaped new tool; published a paper that begins, pompously "Information overload is a major obstacle to scientific progress" as if this system is going to help deal with that, and then goes on to report that the tool achieves 68% on test A, 78.3% on test B and so on; and published a web site which says specifically I can use it to hammer nails, which you are now saying is a deliberate misinterpretation on my part, completely irrelevant to its true value.
