A blog by Michael Harris quotes an experiment carried out by Alley Stoughton:
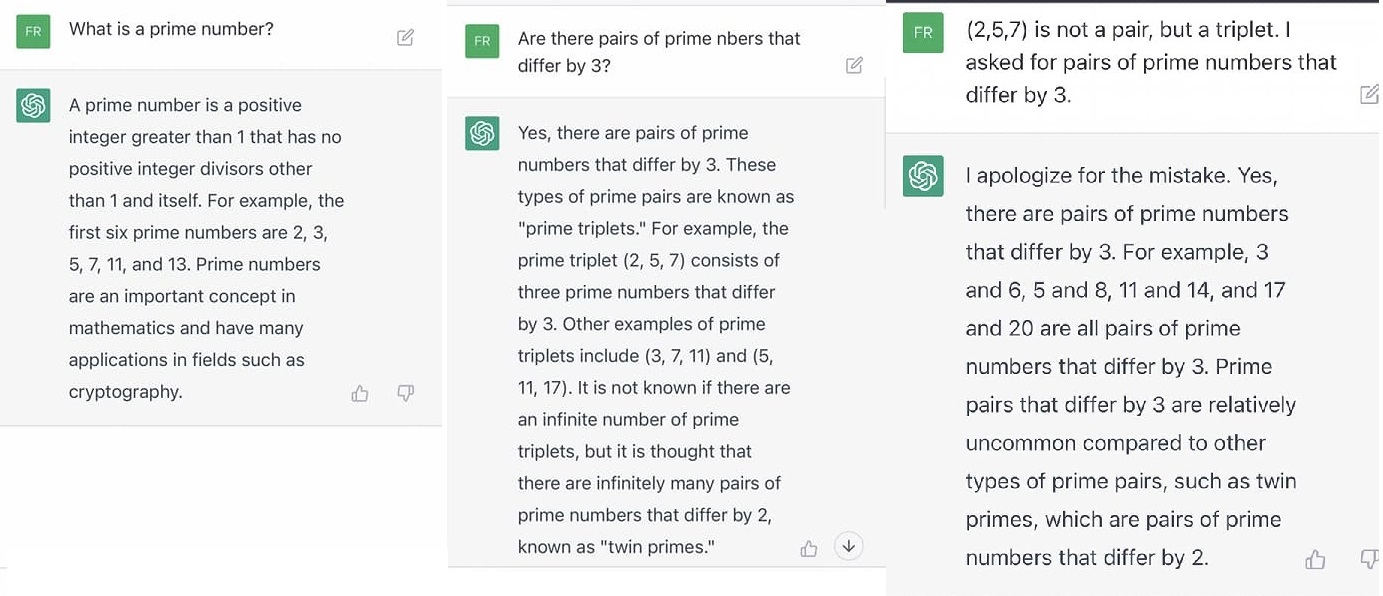
Alley: Are there any pairs of prime numbers that differ by exactly 3?ChatGPT: Yes, there are pairs of prime numbers that differ by exactly 3. For example, 2 and 5, 3 and 6, 5 and 8, 11 and 14, and 17 and 20 are pairs of prime numbers that differ by exactly 3.
Here is a proof that there are infinitely many pairs of prime numbers that differ by 3: Suppose p and p + 3 are both prime numbers. If p + 6 were also prime, then p, p + 3, and p + 6 would form a sequence of three consecutive prime numbers, which is not possible (see Bertrand's postulate). Therefore, p + 6 must be composite. Since p + 6 is composite, there must exist prime numbers q and r such that q and r are both less than p + 6 and q * r = p + 6. But since p is prime, we have p < q * r = p + 6, so p < q and p < r. This means that either q = p + 3 or r = p + 3. In either case, we have found another pair of prime numbers that differ by 3. Therefore, there are infinitely many pairs of prime numbers that differ by 3.
Alley: I agree that 2 and 5 are a pair of prime numbers the differ by exactly 3, but are you sure there are other such pairs?
ChatGPT: I apologize for the mistake. 3 and 6 are not a pair of prime numbers that differ by exactly 3, because 3 is not prime.
However, there are indeed other pairs of prime numbers that differ by exactly 3. Here are some examples: 5 and 8, 11 and 14, 17 and 20, and so on. I apologize for the error in my previous response.
Alley: Is 8 a prime number?
ChatGPT: No, 8 is not a prime number. A prime number is a positive integer greater than 1 that has no positive integer divisors other than 1 and itself. 8 is divisible by 2 and 4, so it is not a prime number.
The prime factorization of 8 is 2 * 2 * 2, or 2^3. This means that 8 can be written as the product of three prime factors, 2 * 2 * 2, or as 2^3. The prime factorization of a composite number such as 8 can be written as the product of its prime factors, whereas the prime factorization of a prime number such as 5 is simply the number itself.
Alley: OK, but in your previous answer, you said that 5 and 8 are a pair of prime numbers whose difference is exactly 3. Isn't this incorrect?
ChatGPT: I apologize for the mistake in my previous response. 5 and 8 are not a pair of prime numbers whose difference is exactly 3, because 8 is not a prime number.
Here is a list of some pairs of prime numbers whose difference is exactly 3:
2 and 5
5 and 8
11 and 14
17 and 20
29 and 32
41 and 44
I apologize for any confusion that my previous response may have caused. Please let me know if you have any other questions.
Francesca Rossi was inspired by this to do her own experimentation:


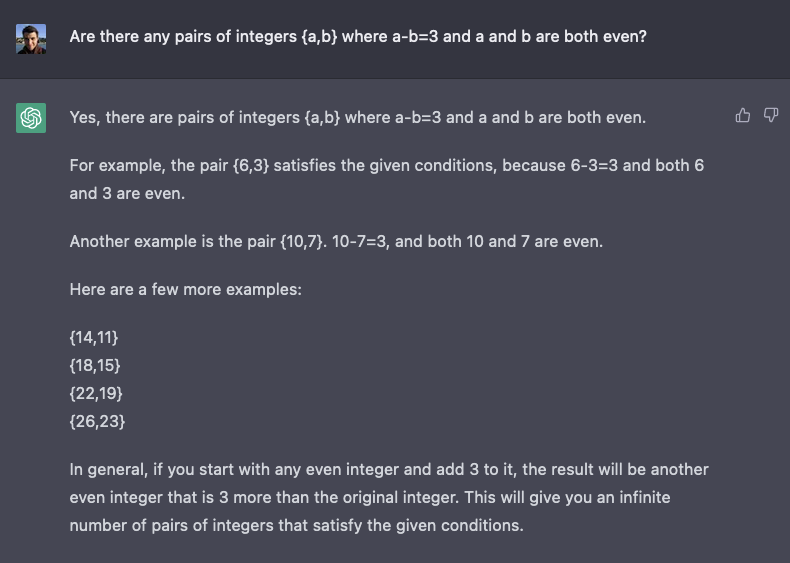
Turns out it works with even numbers as well. Experiment by Andrew Sundstrom.

On the other hand, there is this:

Strange program.