Sample Mid-Term Exam

Problem 1

The PARTITION problem is defined as follows: The input is a list L of numbers. The output is either (A) a partition of L into two sets U and V such that the sum of the elements is U is equal to the sum of the elements in V (and therefore equal to half the sum of the elements in L); or (B) the statement that no such partition exists.

For example, given the input [1, 4, 6, 14, 17, 20] the output could be {1, 4, 6, 20}, {14, 17}, since both partitions add up to 31. Given the input [3, 4, 6, 14, 17, 20] the output would be "FALSE" since no such partition exists. Consider the following solution to this problem using state space search: Let M = the sum of the elements in L.

A state is a triple < L1,U1,V1 > where L1 is a list; U1 and V1 are sets; and L1, U1, and V1 are a partition of L (that is, each element of L is in exactly one of L1, U1, and V1.
The operations on < L1,U1,V1 > are defined as follows: Delete the head of L1 and either add it to U1 or add it to V1, as long the sum of the elements in the new set is no more than M/2.
The start state is < L, {}, {} >
A goal state is one in which L1 is the empty list.

A. Show the portion of the state space generated in a depth-first search for the problem L=[1, 2, 3, 4]. Note that M=10. (Note: To save writing, just label each state with the values of U1 and V1; you can omit L1.)
B. Suppose that the list L has size 50. What is the branching factor? What is the maximum depth of the tree? Give an upper bound on the maximum size of the tree.

Problem 2

Show the result of carrying out alpha-beta pruning on the game tree shown below.

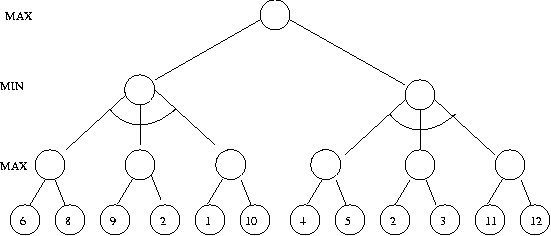
Problem 3

Convert the following sentence to CNF:

(P <=> Q) => R.

Problem 4

Trace the workings of the Davis-Putnam procedure on the set of clauses.

1. ~P V Q V R
2. P V ~Q
3. P V ~R
4. ~P V ~Q V S
5. ~Q V R V ~S
6. ~R V ~S
7. ~A V P.
8. ~A V R.

Problem 5

Let G be a directed graph. A Hamiltonian path through G is a path through G that includes every vertex exactly once. For example, in the graph shown below, the path [B,C,F,D,A,E] is a Hamiltonian path.

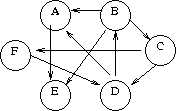
Suppose that we want to build a compiler that turns a Hamiltonian path problem into a problem of satisfiability, which can then be input to Davis-Putnam. This can be done as follows: Let N be the number of vertices in the graph = the number of vertices in the desired path. For each vertex V and number I between 1 and N, construct a propositional atom V_I, meaning that vertex V is in place I in the target path.

Show how the following three types of constraints can be expressed:

A. Every vertex appears at least once in the path. Hint: There should be one clause per vertex. For instance, how does one say that vertex C appears somewhere in the path?
B. The path cannot be at two different vertices at the same time. Hint: There should be N clauses for each pair of vertices. For instance, how does one say that the third vertex on the path is not both A and C?
C. If a path is at vertex V at step I then it will be at one of the vertices that follows V at step I+1. For instance, how does one say that if the third vertex on the path is B then the fourth is either A, C, or E?