Sample problems from 2nd half of course

Let me emphasize that this is just a collection of sample problems, not a sample final exam.

Multiple choice problems

Problem 1

Consider the following CFG grammar:

S -> NP VP
NP -> NG | NG "and" NG
NG -> pronoun | noun
VP -> verb | verb NP | VP "and" VP

Lexicon:
I : pronoun.
cook : noun, verb
eggs : noun
fish : noun, verb.

Which of the following parse tree are correct:

 
i.  S ---> NP ---> NG ---> pronoun ---> I
       |
       |-> VP ---> verb ---> cook
               |
               |-> NP ---> NG ---> noun ---> eggs
                       |
                       |-> "and"
                       |
                       |-> NG ---> noun ---> fish


ii. S ---> NP ---> NG ---> pronoun ---> I
       |
       |-> VP ---> verb ---> cook
               |
               |-> NP ---> NG ---> noun ---> eggs
                       |
                       |-> "and"
                       |
                       |-> VP ---> verb ---> fish


iii.S ---> NP ---> NG ---> pronoun ---> I
       |
       |-> VP ---> VP ---> verb ---> cook
               |       |       
               |       |-> NP ---> NG ---> noun ---> eggs
               |               
               |-> "and"
               |
               |-> VP ---> verb ---> fish


iv. S ---> NP ---> NG ---> pronoun ---> I
       |
       |-> VP ---> verb ---> cook
               |       
               |-> NP ---> NG ---> noun ---> eggs
               |       
               |-> "and"
               |
               |-> VP ---> verb ---> fish

A. All four.
B. Only (i)
C. (i), (iii), and (iv).
D. (i) and (iii).
E. (i) and (iv).

Answer: D.

Problem 2

In a chart parser, the "EXTENDER" module could combine edge [2,4,VP -> VG * NP] with
A. edge [2,4,VG -> modal verb *] to create edge [2,4,VP -> VG NP *]
B. edge [4,6,VG -> modal verb *] to create edge [2,6,VP -> VG NP *]
C. edge [2,6,VG -> modal verb *] to create edge [2,6,VP -> VG * NP]
D. edge[2,4,NP -> determiner noun *] to create edge [2,4,VP -> VG NP *]
E. edge[4,6,NP -> determiner noun *] to create edge [2,6,VP -> VG NP *]
F. edge[2,6,NP -> determiner noun *] to create edge [2,6,VP -> VG * NP]

Answer: E.

Problem 3

Compositional semantics is

A. The principle that the meaning of a sentence is derived by combining the meanings of the words in a mode indicated by the syntactic structure.
B. A technique for applying world knowledge to semantic interpretation.
C. The problem of giving an interpretation to a text of many sentences.
D. A method of disambiguation.
E. The decomposition of a word into a root and its inflections, prefixes and suffixes.

Answer: A.

Problem 4

Bayes' Law states that

A. Prob(P|Q) = Prob(P) / Prob(Q).
B. Prob(P|Q) = Prob(Q|P)
C. Prob(P|Q) = Prob(Q|P) / Prob(Q)
D. Prob(P|Q) = Prob(P) * Prob(Q|P) / Prob(Q)
E. Prob(P|Q) = Prob(Q) * Prob(Q|P) / Prob(P)

Answer: D.

Problem 5

In a feed-forward, back-propagation network, learning proceeds by

A. Propagating activation levels from the input layer to the output layer.
B. Propagating activation levels from the output layer to the input layer.
C. Propagating modification to weights on the arcs from the input layer to the output layer.
D. Propagating modification to weights on the arcs from the output layer to the input layer.
E. Adding nodes and links in the hidden layers.
F. Both adding and deleting nodes and links in the hidden layers.

Answer: D.

Long Answer Problems

Problem 6:

Consider a domain where the individuals are people and languages. Let Z be the first-order language with the following primitives:

s(X,L) --- Person X speaks language L. 
c(X,Y) --- Persons X and Y can communicate. 
i(W,X,Y) --- Person W can serve as an interpreter between persons X and Y.
j,p,m,e,f --- Constants: Joe, Pierre, Marie, English, and French respectively.

A. Express the following statements in Z:

i. Joe speaks English, but Pierre speaks French.
Answer: s(j,e) ^ s(p,f).
ii. If X and Y both speak L, then X and Y can communicate.
Answer: forall(X,Y,L) s(X,L) ^ s(Y,L) => c(X,Y).
iii. If W can communicate both with X and with Y, then W can serve as an interpreter between X and Y.
Answer: forall(W,X,Y) c(W,X) ^ c(W,Y) => i(W,X,Y).
iv. For any two languages L and M, there is someone who speaks both L and M.
forall(L,M) exists(X) s(X,L) ^ s(X,M).
v. Marie can speak both English and French.
s(m,e) ^ s(m,f).
vi. Marie can interpret between Joe and Pierre. i(m,j,p).

B. Show how sentences (i), (ii), (iii), (v), and (vi) can be expressed in Datalog. (Hint: Sentences (i) and (v) each turn into two facts in Datalog.)

Answer: 1. s(j,e).
2. s(p,f).
3. s(X,L) ^ s(Y,L) => c(X,Y).
4. c(W,X) ^ c(W,Y) => i(W,X,Y).
5. s(m,e).
6. s(m,f).
7. i(m,j,p).

C. Explain why sentence (iv) cannot be expressed in Datalog.
Answer: Because Datalog cannot express an existential quantifier.

D. Show how (vi) can be proven from (i), (ii), (iii) and (v) using forward chaining.

Answer: 8. c(m,j). Combining (3) with (5) and (1), substituting X=m, Y=j, L=e.
9. c(m,p). Combining (3) with (6) and (2), substituting X=m, Y=p, L=f.
10. i(m,j,p). Combining (4) with (8) and (9), substituting W=m, X=j, Y=p.

E. Show how (vi) can be proven from (i), (ii), (iii) and (v) using backward chaining.

Answer:

Goal G0: i(m,j,p).  Match with (4) binding W1=m, X1=j, Y1=p.
   Subgoals G1: c(m,j). G2: c(m,p).
  
   Goal G1: c(m,j). Match with (3) binding X2=m, Y2=j.
      Subgoals G3: s(m,L2). G4: s(j,L2)

      Goal G3: s(m,L2). Match with (5) binding L2=e.
      G3 succeeds.

      Goal G4: s(j,e).  Match with (1).
      G4 succeeds.
   G1 succeeds.

   Goal G2: c(m,p). Match with (3) binding X3=m, Y3=p.
      Subgoals: G5: s(m,L3).  G6: s(p,L3).

      Goal G5: s(m,L3). Match with (5) binding L3=e.
      G5 succeeds.

      Subgoal: G6: s(p,e).  No match. G6 fails.

      Return to G5.
      Goal G5: s(m,L3). Match with (6) binding L3=f.
      G5 succeeds.

      Subgoal: G6: s(p,f). Match with (2).
      G6 succeeds.
  G2 succeeds.
G0 succeeds.

Problem 7

Consider the following pair of sentences:
A. Joe wore a wool suit. ("suit" = pants and jacket)
B. The suit is in the court. ("suit" = lawsuit).
Explain how the disambiguation techniques of selectional restriction and frequency in context can be applied in these two sentences.

Answer: Sentence A can be disambiguated using selectional restrictions: The object of "wore" must have the feature CLOTHES which the meaning "lawsuit" does not have. (Actually, there are other meanings of "wore" -- "She wore a smile", "The lecture wore me out" etc. but none that allows a lawsuit as object.)

Sentence B can be disambiguated using frequency in context. The word "court" establishes a context of legal affairs, in which "suit" probably means a law suit.

Problem 8

List the major modules of a natural language interpretation system and explain their function.

Answer:

Morphological analysis identifies the structure of each individual word, separating it into a root word (or words) combined with prefixes, suffixes, and inflections. It is applied to each word separately. The output is a set of morphemes.

Syntactic analysis finds the grammatical structure of each individual sentence, described as a parse tree (plus transformations). The input is a single sentence, plus the output of the morphological analysis on the words of the sentence. The output is a parse tree.

Semantic analysis interprets the meaning of each individual sentence, based on the meanings of the words and the syntax of the sentence. The input is the parse tree constructed by the syntactic analysis. The output is a symbolic representation of the meaning of the sentence.

Discourse/text analysis connects the meanings of the individual sentence to get the overall meaning of the conversation/text.

Problem 9

A. Give an example of a sentence or pair of sentences in which selectional restrictions can be used to disambiguate potential anaphoric ambiguity. Explain the ambiguity and the selectional restriction used.

Answer: There are lots of answers. Here's one. "When I cut the steak with my knife, I found that it was undercooked" (Contrast "... its blade broke off its handle"). "Undercooked" can only modify an object with feature FOOD; hence "it" can be "steak" but not "knife".

B. Give an example of a sentence or pair of sentences in which there is a potential anaphoric ambiguity that cannot be disambiguated using selectional restrictions. Explain why not. Give a method for carrying out the disambiguation.

Answer: "Margaret invited Susan for lunch but she declined." The anaphoric ambiguity of "she" cannot be resolved by selectional restrictions, since Margaret and Susan have all the same features. Rather a rule of world knowledge asserts that if A invites B to do something, then B is likely either to accept or to decline.

Problem 9

Consider the sentence "Hammers are for driving nails into surfaces." Name two words in this sentence that are lexically ambiguous. (There are at least four.) For each of these two words, describe a disambiguation technique which will choose the right interpretation over at least one of the wrong interpretations. Be specific.

Answer:

A. The preposition "for" has many different meanings. Even in the phrase "are for" it can mean:
- i. "are used for" as above.
- ii. "favors" as in "Cheney is for burning more fossil fuel and against conserving resources." This can be ruled out by selectional restrictions: this meaning requires an animate subject, unlike "hammers".
- iii. "are intended to be given to" as in "The presents are for the baby." This can be ruled out by selectional restrictions: it requires an animate object, unlike "driving".
B. "driving" can mean:
- i. forcing an object to move against resistance, as above.
- ii. driving a car (by far the most frequent meaning).
- iii. impelling a person to undesired behaviors (as in "driving me crazy", "driving me to drink")
- quite a few other specialized meanings (iv. "driving" in golf, v. "driving cattle", etc.)
However, most of these can be ruled out by selectional restrictions on the object. E.g. (ii) requires a car as object; (iii) and (v) require animate objects, etc.
C. "nails" can be either the tool or fingernails. However, frequency in the context of "hammer" gives a preference for the tool.
D. "into" can mean
- i. motion into the interior of a region, as in "He drove the nail into the board".
- ii. motion through a boundary into the interior of another region, as above.
- iii. "in the direction of" as in "He looked into the sun".
- iv. "against" as in "He ran into a brick wall".
Here, I think, one has to rely on world knowledge that a hammer is used to drive a nail through the surface of an object into its interior.

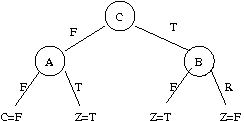
Problem 10 (10 points)
In this problem and in problem 11, we consider a data set with three Boolean predictive attributes, A,B,C, and a Boolean classification, Z.

A. Suppose that your data is completely characterized by the following rules:

1. If X.A = T and X.C = F then X.Z = T.
2. If X.B = F and X.C = T then X.Z = T.
3. Otherwise, X.Z=F.

Construct a decision tree whose predictions correspond to these rules.

B. True or false: Given any consistent set of rules like those above, it is possible to construct a decision tree that executes that set of rules. By "consistent", I mean that there are no examples where two different rules give different answers.

Answer: True. At the worst, one can use the complete decision tree, where all tests on all attributes are made, and so each different instance is represented by one leaf.

Problem 11 (5 points)
Which of the following expresses the independence assumption that is used in deriving the formula for Naive Bayesian learning, for the classification problem in problem 3.

a. Prob(Z|A,B,C) = Prob(Z|A) * Prob(Z|B) * Prob(Z|C)
b. Prob(Z|A,B,C) = Prob(A,B,C | Z) * Prob(Z) / Prob(A,B,C)
c. Prob(A,B,C|Z) = Prob(A|Z) * Prob(B|Z) * Prob(C|Z)
d. Prob(A,B,C) = Prob(A) * Prob(B) * Prob(C)
e. Prob(Z|A,B,C) = Prob(Z|A) * Prob(A|B) * Prob(B|C).
f. Prob(A,B,C|Z) = Prob(A|Z) * Prob(B|A) * Prob(C|B).

Answer: c. (b) is Bayes' Law, which is used, but is not an independence assumption. (d) and (f) are independence assumptions, but not the ones we need. (a) and (e) are junk.

Problem 12 (10 points)
Consider the following data set T. A and B are numerical attributes and Z is a Boolean classification.

Find a set of weights and a threshhold that categorizes all this data correctly. (Hint: Sketch a graph of the instances in the plane where the coordinates are A and B.)

Answer: w_A=0, w_B=1, T=1.5 will do fine.