Converting Combinatorial Problems to Satisfiability: Some Examples
Hamiltonian Path
Given an undirected graph, find a path containing every vertex exactly
once. For instance, in the graph shown below, one solution would be the path
[A,E,B,C,F,G,D,H]

Translation to propositional logic
Atoms have the form Path(V,I) for each vertex V and for
I ranging from 1 to }V}, the number of vertices. In the above
example, there would be 64 atoms Path(A,1), Path(A,2) ...
Path(H,7), Path(H,8).
There are four kinds of constraints necessary:
-
Each vertex appears at some index. For instance, in the above example
one such constraint would be
Path(A,1) V Path(A,2) V ... V Path(A,8).
-
No two vertices appear at the same index. For instance, in the above
example, one such constraint would be
¬[Path(A,1) ^ Path(B,1)]
- A vertex cannot appear in two different indices. For instance, in
the above example, one such constraint would be
¬[Path(A,1) ^ Path(A,2)]
-
Two vertices in sequence on the path must be connected by an edge in
the graph. This can be encoded in either of two ways:
A. If U is in position I, then the vertex in position I+1 must be one of
those connected by one of the edges. In the above example, taking U to be
D and I to be 3, the constraint would be
Path(D,3) → [Path(C,4) V Path(G,4) V Path(H,4)].
B. If U is in position I and there is no edge U-V, then V is not in
position I+1. in the above example, taking U to be D, V to be A, and I
to be 3, the constraint would be
¬[Path(D,3) ^ Path(A,4)]
The following constraint is not needed, because it follows logically
from the above, but might well be helpful in speeding up search.
-
Every index includes a vertex. In the example above, one such constraint
would be
Path(A,1) V Path(B,1) V ... V Path(H,1).
Map coloring
The map coloring problem is this: You are given an undirected graph and
a set of colors. The goal is to assign a color to every vertex so that no
two vertices connected by an edge have the same color.
This picture shows a 4-coloring of the continental US states. (The vertices
are the states and two vertices have an edge between them if they border
geographically.)
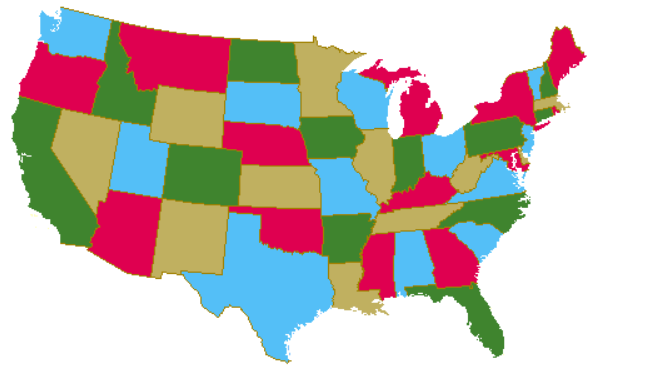
(Problem to think about: Prove that for this map there is no solution that uses 3
colors. Hint: Think about Nevada and the states that it borders.)
This can be translated into the propositional calculus as follows:
Atoms have the form Color(V,C) meaning that vertex V is assigned
color C. In the above map, there would be the atoms Color(Alabama,Blue),
Color(Alabama,Green) ... Color(Wyoming,Red).
There are two types of necessary propositions.
- Every vertex is assigned a color. In this example, one such constraint
would be
Color(Alabama,Blue) V Color(Alabama,Bronze)`V Color(Alabama,Green) V
Color(Alabama,Red).
- No two adjacent vertices are assigned the same color. In this example
this examples, two such constraints would be
¬[Color(Alabama,Blue) ^ Color(Arkansas,Blue)].
¬[Color(Wyoming,Red) ^ Color(Utah,Red)].
This can yield solutions where one country has more than one color, but if
so, you can choose either arbitrarily, since neither will be the same as
any color of any neighboring country.
Optional constraint that may speed processing:
- Each country has only one color. In this example
¬[Color(Alabama,Red) ^ Color(Alabama,Blue)]
