Dynamics of Complex Fluids


Complex fluids are fluids -- usually Newtonian -- that have suspended microstructure such as long-chain polymers, microscopic rods and fibers, colloidal particles, or even swimming bacteria. Understanding the mechanical responses of complex fluids is important to contemporary problems -- micro-fluidic mixing, transport, separation -- in engineering, physics, and biology. The interesting and difficult character of these systems lies in their multi-scale reciprocal coupling: immersed particles react to the large-scale fluid flow -- changing shape, changing direction of motion, orientation, stretching, interacting -- and so produce fluid stresses that feed back and modify the large-scale flow. Research on complex fluids within the CMCL focusses on their dynamics both at the level of microstructure, and at the macroscopic scale.

Dynamics of Active Suspensions
A simulation of orientational instability in 3D suspension of self-locomoting rods

 The mixing of a dye field by the instability of an active suspension from isotropy

Suspensions of self-propelled particles, such as swimming microorganisms, are known to undergo complex dynamics as a result of hydrodynamic interactions. Understanding these dynamics are important to the application of active particle suspensions, whether synthetic or biological, to microfluidic mixing and transport. We have developed both particle-based and continuum approaches to simulating and analyzing active suspension dynamics.  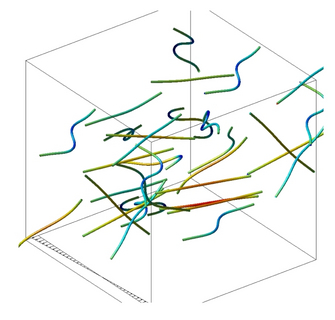For example, the figure at upper left shows a simulated dynamics of a 3D suspension of self-locomoting rods. In agreement with previous theoretical predictions, orientationally ordered suspensions of such swimming particles are found to be unstable at long wavelengths as a result of hydrodynamic fluctuations. The long-time dynamics is one of system-scale isotropy, short-range alignment, and rapid fluid mixing.
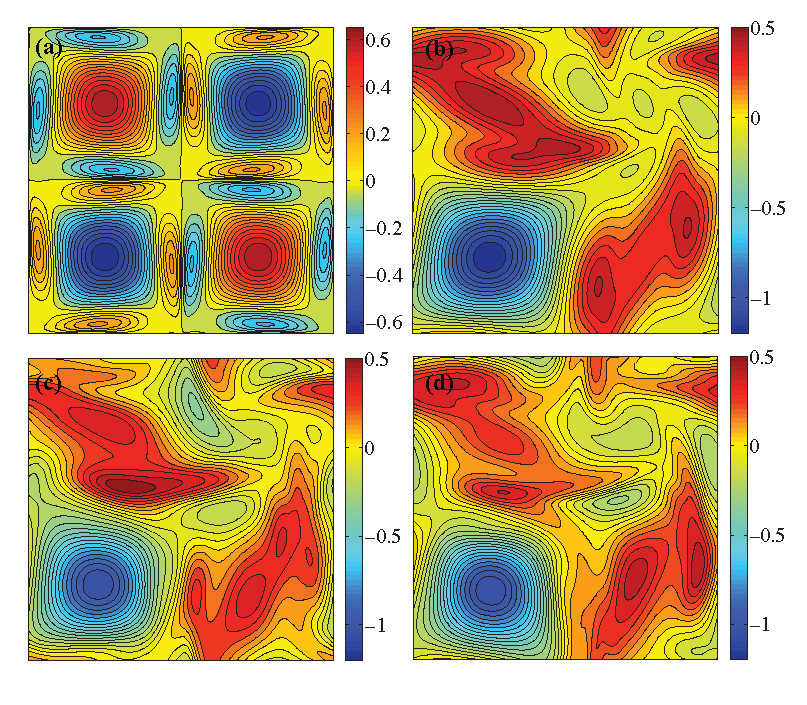
    To extend our understanding of these dynamics, we have also developed a hydrodynamic theory and applied to study linear stability and the nonlinear pattern formation. For isotropic suspensions, we demonstrate the existence of an instability for the active particle stress, in which shear stresses are eigenmodes and grow exponentially at long scales. Nonlinear effects are also investigated using numerical
simulations in two dimensions. The long-time nonlinear behavior is shown to be characterized by the formation of strong density
fluctuations, which merge and breakup in time in a quasiperiodic fashion. The figure at upper right shows that these complex motions
result in very efficient fluid mixing.

Other areas of study include the linear well-posedness of our continuum theory, the development of a simulator for suspensions of non-slender self-propelled bodies, and the hydrodynamic properties of self-assembled helical swimmers.

For technical references see:

Transport and Mixing of Viscoelastic Fluids
Polymer stress in the transport of a viscoelastic fluid via peristaltic pumping
 Mixing dynamics in a viscoelastic flow driven by a time-independent force

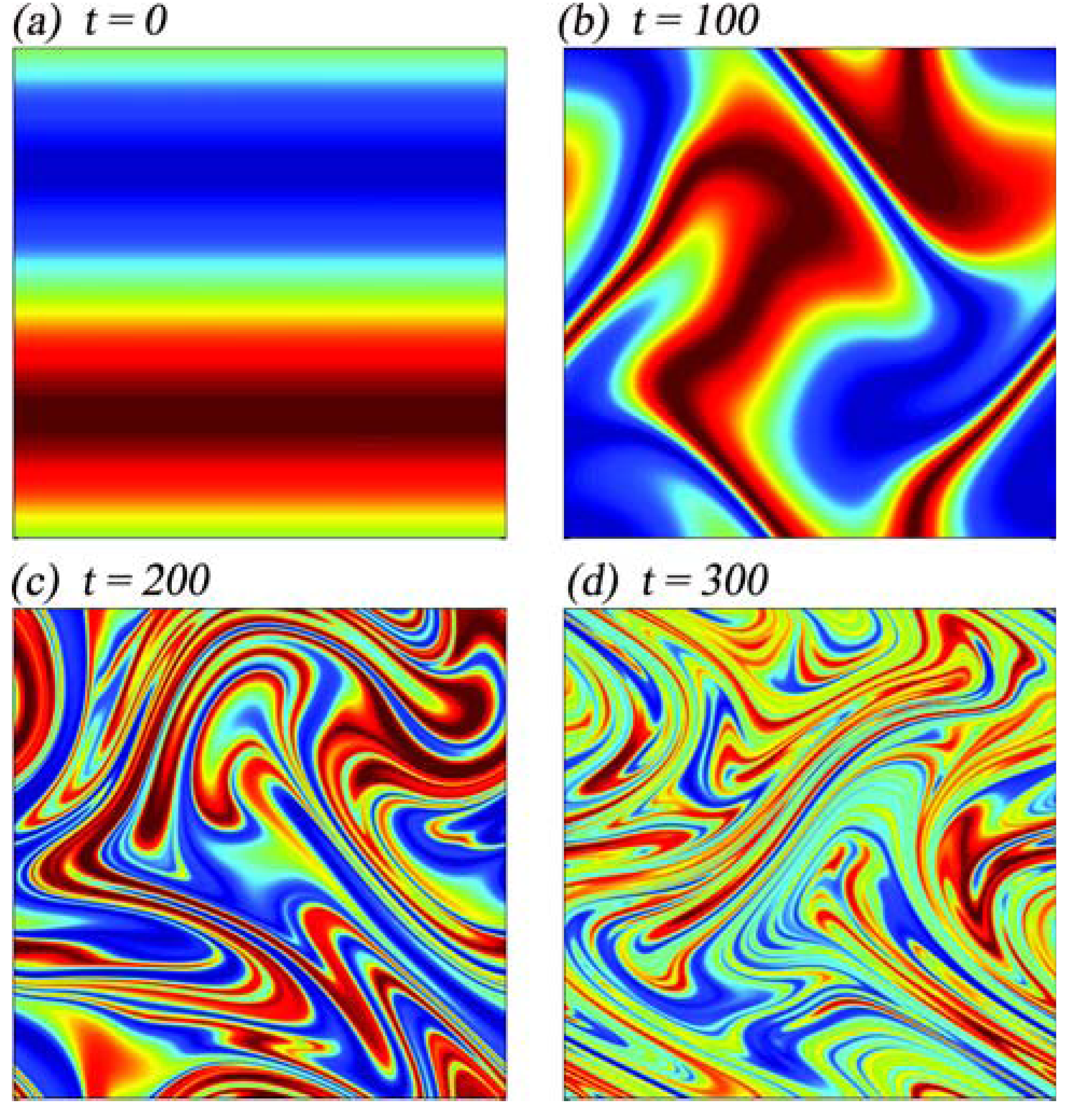
The dynamics of viscoelastic fluids is remains poorly understood, even in the regime of low Reynolds number (Re), the common setting for many biological and technological flows. An interesting aspect of viscoelasticity is its introduction of nonlinearity and finite memory to low Re flow, destroying Stokes reversibility, and in some cases allowing behaviors more reminiscent of high Re. We have been studying the dynamics where these aspects are central.
    The figure on upper left shows the development of large normal stresses in a simulation of a viscoelastic fluid being pumped through a channel by peristaltic waves. Peristalsis is a fundamental mode of fluid transport in engineered and biological systems. The normal stress develop on time-scales set by the Weissenberg number (Wi, the ratio of polymer relaxation time to the flow time-scale), and for sufficiently large Wi can be driven by a coil-stretch transition. Our simuation reveals that these polymer stresses create large forces on the channel walls, and create a strong reflux against the driven flow, severely decreasing the pump's efficiency.
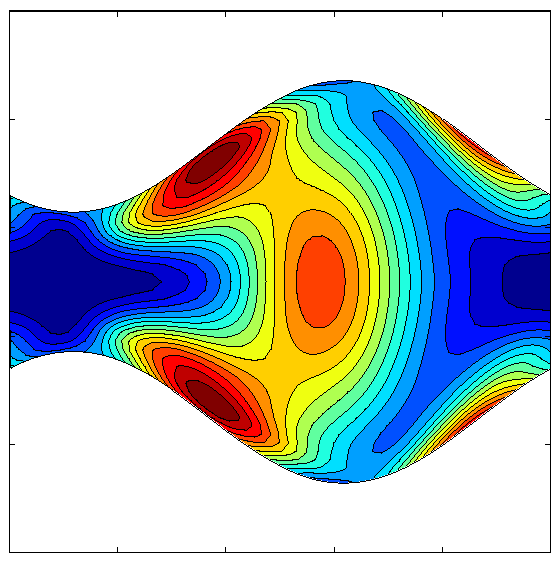
    The figure at right shows that quasi-periodic mixing dynamics can arise in viscoelastic flows, even at zero Re. This is a simulation of the Oldroyd-B model where the fluid is being driven by a time-independent force that in the absence of the polymer field, would create a time-independent, four-roll mill vortical flow. Here the dynamics follows from a symmetry-breaking instability that happens for sufficiently large Wi.

Other areas of study include the simulation of 3D mixing dynamics, and the swimming of undulating bodies in viscoelastic fluids.

For technical references see:
Dynamics of Fiber Suspensions
Interacting flexible filaments immersed in a Stokesian fluid
 A flexible fiber in a Stokesian fluid performing a random walk as a consequence of the stretch-coil instability

The understanding of the dynamics of such fiber suspensions are fundamental to understanding many flows arising in physics, biology and engineering. Examples include fiber-reinforced composites, the dynamics and rheology of biological polymers and the motility of microscopic organisms. Such filaments often have aspect ratios of length to radius ranging from a few hundred to several thousand. Full discretizations of such thin objects in a 3D domain is very costly. The Reynolds numbers for these applications typically very low.
    We have constructed simulation methods for multiple flexible fibers immersed and interacting in a 3D Stokesian fluid. These methods make explicit use of the special nature of the Stokes equations, as well as the slenderness of the fibers. The key points are that boundary integral methods can be employed to reduce the three-dimensional dynamics to the dynamics of the two-dimensional filament surfaces, and that using slender body asymptotics, this can be further reduced to the dynamics of the one-dimensional filament centerlines. The resulting intergral equations take into account the fluid-filament interaction as well as filament-filament interactions, as mediated by the fluid. The figure at left shows the dynamics of many interacting fibers immersed in an oscillating shear, a common rheological flow for measure the complex moduli of elastic fluids. These fibers have undergone a buckling instability kicked off by hydrodynamic interactions amongst them.
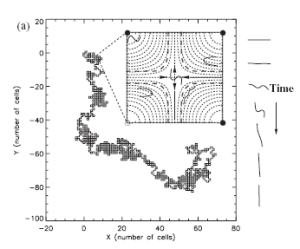
    We have also uncovered new instabilities in fiber suspensions that lead to microstructural transport. The figure at right shows the wandering orbit of a flexible fiber immersed in a cellular flow. At the heart of this dynamics is the stretch-coil instability, which is the analog of the classical coil-stretch instability of polymeric fluids. The stretch-coil instability is a buckling instability driven by the compressional flows in the neighborhood of flow stagnation points.

Other areas of studies include the dynamics of rigid fiber suspensions, the development of fast summation methods for many particle dynamics in the Stokes equations.

For technical references see