Michael L. Overton
Draft for Encyclopedia Americana
December 20, 1997
LINEAR PROGRAMMING, a specific class of mathematical problems, in which a linear function is maximized (or minimized) subject to given linear constraints. This problem class is broad enough to encompass many interesting and important applications, yet specific enough to be tractable even if the number of variables is large.
History. Linear programming was developed as a discipline in the 1940's, motivated initially by the need to solve complex planning problems in wartime operations. Its development accelerated rapidly in the postwar period as many industries found valuable uses for linear programming. The founders of the subject are generally regarded as George B. Dantzig, who devised the simplex method in 1947, and John von Neumann, who established the theory of duality that same year. The Nobel prize in econonmics was awarded in 1975 to the mathematician Leonid Kantorovich (USSR) and the economist Tjalling Koopmans (USA) for their contributions to the theory of optimal allocation of resources, in which linear programming played a key role. Many industries use linear programming as a standard tool, e.g. to allocate a finite set of resources in an optimal way. Examples of important application areas include airline crew scheduling, shipping or telecommunication networks, oil refining and blending, and stock and bond portfolio selection.
Overview. The general form of a linear program is
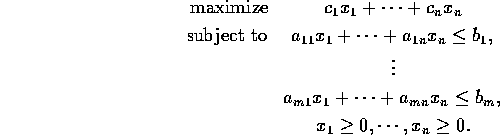
Here ![]() ,
, ![]() and
and ![]() are given numbers, and
are given numbers, and ![]() are variables whose values
are to be determined, maximizing the given objective
subject to the given constraints. There are n variables and m
constraints, in addition to the nonnegativity restrictions on
the variables. The constraints are called linear because they
involve only linear functions of the variables. Quadratic terms such
as
are variables whose values
are to be determined, maximizing the given objective
subject to the given constraints. There are n variables and m
constraints, in addition to the nonnegativity restrictions on
the variables. The constraints are called linear because they
involve only linear functions of the variables. Quadratic terms such
as ![]() or
or ![]() are not permitted. If minimization is
desired instead of maximization, this can be accomplished by reversing
the signs of
are not permitted. If minimization is
desired instead of maximization, this can be accomplished by reversing
the signs of ![]() .
.
An example is very helpful. Consider the linear program

where the numbers ![]() and
and ![]() , defining the maximization objective
, defining the maximization objective
![]() , have not yet been specified.
In this example, n, the number of variables, is 2, and m, the
number of constraints, is 3
In Figure 1, each constraint is shown by a straight line, with one
side of the line shaded to indicate that the points
, have not yet been specified.
In this example, n, the number of variables, is 2, and m, the
number of constraints, is 3
In Figure 1, each constraint is shown by a straight line, with one
side of the line shaded to indicate that the points ![]() on that
side of the line do not satisfy the corresponding constraint.
The central unshaded region in Figure 1 is the set of points
on that
side of the line do not satisfy the corresponding constraint.
The central unshaded region in Figure 1 is the set of points ![]() which satisfy all the constraints. This is called
the feasible region. The boundary of the feasible region is a polygon.
which satisfy all the constraints. This is called
the feasible region. The boundary of the feasible region is a polygon.
Now consider the problem of maximizing the linear function
![]() , for given numbers
, for given numbers ![]() ,
, ![]() , over points
, over points ![]() lying in the feasible region. The quantity
lying in the feasible region. The quantity ![]() is called
the objective function.
If
is called
the objective function.
If ![]() , the goal is to maximize
, the goal is to maximize ![]() , and
it is clear from Figure 1 that this is achieved by
, and
it is clear from Figure 1 that this is achieved by ![]() .
This point is called the optimal solution. On the other hand,
if
.
This point is called the optimal solution. On the other hand,
if ![]() ,
, ![]() , the goal is to maximize
, the goal is to maximize ![]() , and the
optimal solution is
, and the
optimal solution is ![]() . If
. If ![]() ,
, ![]() , the goal
is to maximize
, the goal
is to maximize ![]() , and the optimal solution is any point on the line
segment between (2,1) and (2,2).
It is intuitively clear that regardless of the values of
, and the optimal solution is any point on the line
segment between (2,1) and (2,2).
It is intuitively clear that regardless of the values of ![]() ,
, ![]() ,
the optimal solution is on the boundary of the feasible region.
For most choices of
,
the optimal solution is on the boundary of the feasible region.
For most choices of ![]() ,
, ![]() , the optimal solution is unique,
specifically at a vertex of the feasible region,
i.e. one of the corners of the boundary.
, the optimal solution is unique,
specifically at a vertex of the feasible region,
i.e. one of the corners of the boundary.
Not every linear program has an optimal solution. It may happen that no solution exists, either because the feasible region is infinitely large, or because it is empty. For n;SPMgt;2, the feasible region is a polyhedron in n dimensions, possibly infinitely large or empty. If an optimal solution exists, there must always be one at a vertex of the polyhedron, though it is not always unique.
The most remarkable mathematical property of linear programs is the theory of duality. The dual of the linear program given above is

This is a linear program in the variables ![]() . It is not hard to
show that if
. It is not hard to
show that if ![]() is in the feasible region for the first
linear program and
is in the feasible region for the first
linear program and
![]() is in the feasible region for the dual linear program, than
the first objective function
is in the feasible region for the dual linear program, than
the first objective function ![]() is less than
or equal to the dual objective function
is less than
or equal to the dual objective function ![]() .
The remarkable fact is that these two objectives are always
equal for any
.
The remarkable fact is that these two objectives are always
equal for any ![]() and
and ![]() which are, respectively, optimal solutions for the two linear programs.
This is of great practical importance for both the interpretation
of the solutions of linear programs and the methods for calculating their
solutions.
which are, respectively, optimal solutions for the two linear programs.
This is of great practical importance for both the interpretation
of the solutions of linear programs and the methods for calculating their
solutions.
The simplex method. The simplex method has been the standard technique for solving a linear program since the 1940's. In brief, the simplex method passes from vertex to vertex on the boundary of the feasible polyhedron, repeatedly increasing the objective function until either an optimal solution is found, or it is established that no solution exists. In principle, the time required might be an exponential function of the number of variables, and this can happen in some contrived cases. In practice, however, the method is highly efficient, typically requiring a number of steps which is just a small multiple of the number of variables. Linear programs in thousands or even millions of variables are routinely solved using the simplex method on modern computers. Efficient, highly sophisticated implementations are available in the form of computer software packages.
Interior-point methods. In 1979, Leonid Khaciyan presented the ellipsoid method, guaranteed to solve any linear program in a number of steps which is a polynomial function of the amount of data defining the linear program. Consequently, the ellipsoid method is faster than the simplex method in contrived cases where the simplex method performs poorly. In practice, however, the simplex method is far superior to the ellipsoid method. In 1984, Narendra Karmarkar introduced an interior-point method for linear programming, combining the desirable theoretical properties of the ellipsoid method and practical advantages of the simplex method. Its success initiated an explosion in the development of interior-point methods. These do not pass from vertex to vertex, but pass only through the interior of the feasible region. Though this property is easy to state, the analysis of interior-point methods is a subtle subject which is much less easily understood than the behavior of the simplex method. Interior-point methods are now generally considered competitive with the simplex method in most, though not all, applications, and sophisticated software packages implementing them are now available. Whether they will ultimately replace the simplex method in industrial applications is not clear.
An essential component of both the simplex and interior-point methods is the solution of systems of linear equations, which use techniques developed by C.F. Gauss and A. Cholesky in the 18th and 19th centuries. (see LINEAR EQUATIONS and MATRIX). Important generalizations of linear programming include integer programming, quadratic programming, nonlinear programming and stochastic programming (See OPERATIONS RESEARCH).
REFERENCES