|
Home
General Announcement
Program
Principal Lecturer
János Pach
Subject
Geometric Graph Theory
Lectures
Other Invited Speakers
Invited Talks
Participants
Local Arrangements
Computing Facilities
Application Forms
Contacts |
|
May 28 - June 1, 2002
Gateway Center
University of North Texas, Denton
Geometric Graph Theory
The first genuine monograph on graph theory (König, 1936)
had the following subtitle: Combinatorial Topology of
Systems of Segments [K]. Although graph theory and topology
stem from the same root, the connection between them has
somewhat faded away in the past few decades. In the most
prolific new areas of graph theory including Ramsey theory, extremal
graph theory and random graphs, graphs are regarded as
abstract binary relations rather than systems of segments.
It is quite remarkable that traditional graph theory is
often incapable of providing satisfactory answers for the
most natural questions concerning the drawings of graphs.
Geometric Graph Theory is a relatively new discipline at the
borderline of discrete mathematics and computer science, which was
developed to deal with such questions. During the past 10 years
Geometric Graph Theory has played a significant role in settling
and solving several fundamental problems of combinatorial and
computational geometry. We believe that a better understanding
of this field will be crucial in answering many other important
questions in discrete mathematics and in the theory of computing.
A geometric graph
G = (V(G),E(G))
is a graph drawn in the plane by line segments, i.e.,
V(G)
is a set of
points in the plane, no three of which are collinear, and
E(G)
is a set of segments whose endpoints belong to
V(G).
A topological graph is defined similarly,
except that its edges can be arbitrary Jordan curves
connecting two elements of
V(G)
and not passing through a
third vertex. Two edges of a topological (or a geometric)
graph are said to cross if they have a point in
common, different from their endpoints.
The study of geometric graphs was initiated by Erdos
[AE], Avital and Hanani [AH], Perles [AP]
and Kupitz [Ku] more than 30 years ago.
In the early eighties, topological and geometric
graphs were intensively studied by the theoretical computer
science community, due to their applications in VLSI design.
In 1989, during the Special Year on Discrete
and Computational Geometry at DIMACS, Perles gave a
one-semester course on the subject. János Pach, at the
time a Visiting Professor at DIMACS, attended these lectures,
became interested in the topics and soon became one of the
leading experts in this area.
One of the main objectives in geometric graph theory is to
characterize all possible crossing patterns determined by
the edges of a given geometric graph [G1,T2] or, more
generally, by a collection of continuous arcs (``strings'')
in the plane. We are very far from having satisfactory
solutions to these problems, but the existing results are
truly fascinating! They are intimately related to
fundamental results in topology [HLS,RS], in linear
algebra, in the theory of block designs [BF],
and in extremal set theory [EH]. They have many applications
to problems in combinatorial and computational geometry,
including the
k-set problem [ELSS], proximity
problems [S], and the problem of bounding the number
of incidences between elementary geometric objects such as
points and lines, curves, surfaces [PSo,ST1,CEG].
There are two famous old unsolved problems dealing with
crossings: Turán's Brick-Factory Problem [T1] and
Conway's Thrackle Conjecture [W].
The Brick Factory problem (which came to Turán's mind
at a factory yard, where, as forced labour during World War
II, he moved wagons filled with bricks from kilns to
storage places) can be formulated as follows.
Given an abstract graph G,
find a drawing of
G
(i.e., a topological graph isomorphic to
G)
for which the
number of crossings is minimum. This number is called the
crossing number of
G
and is denoted by
cr(G).
Specifically, Turán's (still unsolved) original problem was
to determine
cr(Kn,m),
for the complete bipartite graph
Kn,m
with
n
and
m
vertices in its classes, for every
n, m
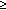 3.
According to an assertion of Zarankiewicz, which
was down-graded from a theorem to a conjecture [G], we have
3.
According to an assertion of Zarankiewicz, which
was down-graded from a theorem to a conjecture [G], we have
This conjecture is still open. In fact, we do not know even
the limits
for
Kn,n
and for the complete graph
Kn.
A thrackle is a topological graph so that any two
edges have exactly one point in common:
they either meet at a common endpoint or they cross.
Conway's conjecture states that the number of edges of a
thrackle cannot exceed the number of vertices. At first
glance this may appear to be just an innocent puzzle
from recreational mathematics. However, this is likely to
represent the tip of a huge iceberg, and a solution
to the problem will probably take us several steps closer
to understanding the structure of crossings,
which may be viewed as a planar analogue of Knot Theory.
Lovász, Pach, and Szegedy [LPS], who verified the conjecture up
to a multiplicative factor of 2, found that parity arguments
play an important role in this subject, just like in the
case of the Brick Factory Problem.
There is a remarkable theorem of Hanani
[H] and Tutte [T2] behind this phenomenon: if any
two edges of a topological graph, not incident to the same
vertex, cross an even number of times, then the
underlying ``abstract'' graph is planar, i.e., it can be
drawn with no crossings.
Crossing numbers have also been studied in theoretical
computer science due to their applications in VLSI design.
In the early eighties, Leighton [L,BL]
and others proved that the chip area required for the
realization of an electrical network is closely related to
the crossing number of the underlying graph.
This discovery gave an impetus to
research in the subject. It was soon realized that main
difficulty in this problem is that a graph has so many
essentially different drawings that the computation of
the crossing number, even for a graph of only 15 vertices,
appears to be a hopelessly difficult task. Garey and
Johnson proved that the determination of the crossing number
is NP-complete [GJ]. Therefore, approximating algorithms,
heuristic methods, and general estimates play important
roles in the subject.
One of the most applicable estimates for crossing numbers
is an inequality discovered by Ajtai, Chvátal,
Newborn, and Szemerédi [AC], and independently by
Leighton [L]: The crossing number of any graph with
n
vertices and
e > 4n
edges is at least a constant times
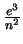 .
The best known value of the constant was found by Pach and
Tóth [PT]. A fundamental result of Pach, Spencer,
and Tóth [PST] settled an old conjecture of Erdos
and Guy [EG] by showing essentially
that there exists an ``asymptotically best constant'' for
which this inequality holds as
n
tends to infinity, no matter how fast
e
goes to infinity at the same time.
They also improved the inequality for special classes of
graphs having some monotone properties. Their estimates
are asymptotically tight and generalize to graphs drawn on
other surfaces. .
The best known value of the constant was found by Pach and
Tóth [PT]. A fundamental result of Pach, Spencer,
and Tóth [PST] settled an old conjecture of Erdos
and Guy [EG] by showing essentially
that there exists an ``asymptotically best constant'' for
which this inequality holds as
n
tends to infinity, no matter how fast
e
goes to infinity at the same time.
They also improved the inequality for special classes of
graphs having some monotone properties. Their estimates
are asymptotically tight and generalize to graphs drawn on
other surfaces.
It was a surprising discovery by Székely [S] that
this lower bound easily implies a number of famous theorems of
Beck, Chung, Szemerédi, Trotter and others
[Be1,C,ST1,ST2,CST,SST,CEG] concerning some hard
questions of Erdos in Combinatorial Geometry. In
particular, it yields that the number of unit distances
determined by
n
points in the plane is
O(n4/3).
Shortly after, Dey [D] proved that the same approach can be
used for establishing an
O(n4/3)
bound for the
number of different ways of splitting a set of
n points
in the plane into two equal parts by a line. This was a sensational
improvement of an old result of Lovász [Lo], with many
important applications in Computational Geometry.
We emphasize that this problem or, more generally, the
problem of bounding the number of
k-element subsets
("k-sets") of an
n-element point set in
d-space,
which can be separated from the remaining points by a hyperplane,
arises in the analysis of virtually every geometric algorithm
dealing with arrangements of points and hyperplanes.
Another exciting recent development in this
field is that, using the same technique, Solymosi and
Tóth [SoT] have improved an important theorem of Chung,
Szemerédi and Trotter [CST], and Székely [S].
They showed that any set of
n
points in the plane determines
at least
 (n6/7)
distinct distances.
One may hope that this bound can be improved to about
(n6/7)
distinct distances.
One may hope that this bound can be improved to about
 (n8/9)
using the current methods. However,
this would still be very far from the conjectured optimum,
which is about
(n8/9)
using the current methods. However,
this would still be very far from the conjectured optimum,
which is about
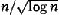 . .
There is another lower bound on the crossing number, derived by
Leighton, which follows from a weighted version of the
Lipton-Tarjan Separator Theorem [LT] for planar graphs.
The bisection width of an abstract graph
G, denoted by
b(G),
is the minimum number of edges whose removal partitions
the vertex set into two parts such that there are no edges
running between them and the larger set has at most twice as
many vertices as the smaller. According to a more general form
of Leighton's inequality, proved by Pach, Shahrokhi and Szegedy
[PSS], the bisection width of any graph
G
with
n
vertices satisfies
where
d1,
d2,
. . .,
dn
denote the degrees of the
vertices. This result has many applications in
computer graphics, computational geometry and graph drawing.
For illustration, we mention a few examples.
I. Souvaine and Wenger studied the following problem
arising in cartography [SW].
Given two disjoint rectangles
P
and
Q
in the plane, containing the points
{
p1,
p2,
. . .,
pn
}
and
{
q1,
q2,
. . .,
qn
},
respectively, we would like to
construct a piecewise linear isomorphism from
P
to
Q,
which maps
pi
to
qi
for every
i.
The objective is to minimize the complexity of such an
isomorphism, i.e., the number of linear pieces it consists
of. Souvaine and Wenger [SW] designed an algorithm for
constructing an isomorphism with complexity
O(n2).
Pach, Shahrokhi and Szegedy [PSS] applied
(*)
to show that this bound cannot be improved.
II. Pach and Wenger [PW] proved that every planar graph
with
n
vertices can be drawn in the plane so that the
positions of the vertices are arbitrarily prescribed, and
each edge is represented by a polygonal path consisting of at
most
24n
segments. The inequality
(*)
can be used to
show that this result, too, is essentially tight.
III. Shahrokhi et al [SSS] applied
(*)
to analyze
an efficient algorithm for constructing a geometric graph
isomorphic to a given abstract graph
G
such that the
number of crossings is
O(
log4
ncr(G))
and the coordinates
of all vertices are integers bounded by
O(n2).
Even et al [EGS] have recently improved this analysis.
In some sense, these results show that the simplest geometric
and topological graphs isomorphic to
G
cannot be drastically
different.
IV. M. Watanabe posed the following problem.
Suppose we have a self-intersecting closed polygon
P
on the screen of our computer, whose vertices are
p1,
p2,
. . .,
pn
in this order, and no three vertices are
collinear. We are allowed to modify
P
so that in each step
we can grab a vertex and move it to an arbitrary new position.
Is it true that every polygon
P
can be untangled,
i.e., turned into a noncrossing polygon, in at most
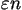 steps, for some absolute constant steps, for some absolute constant
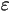 < 1?
Using
(*),
Pach and Tardos [PT]
proved that the answer is in the negative.
< 1?
Using
(*),
Pach and Tardos [PT]
proved that the answer is in the negative.
V. A set of pairwise crossing edges in a geometric or
topological graph is called a crossing set.
Pach, Shahrokhi, and Szegedy [PSS] used
(*)
to prove that if a geometric graph with
n
vertices has no crossing set of size
k,
then its number of edges is
at most
3n(10 log n)2k - 2.
Valtr [V] improved this
result by reducing the exponent of the logarithmic factor to 1.
It is conjectured that for any
k
there exists a constant
ck
such that any geometric graph with no crossing set of size
k
has at most
ckn
edges. For
k = 2
this follows from Euler's Polyhedral Formula, and for
k = 3
it has been verified
by Agarwal et al [AAP]. A closely related conjecture is that
any complete geometric graph with
n
vertices has a crossing set of size
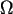 (n).
Aronov et al [AEG]
proved the existence of a crossing set of size
(n).
Aronov et al [AEG]
proved the existence of a crossing set of size
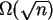 . .
One of the most prolific and most applicable areas of
(abstract) graph theory is Extremal Graph Theory [B],
which was started by Turán's theorem on the maximum
number of edges that a graph with
n
vertices can have without
containing a complete subgraph with
k
vertices.
It is interesting to note that (V) suggests that by asking analogous
questions in a geometric setting, one may obtain exciting
difficult problems, whose solutions require new techniques.
Two edges of a geometric graph are said to be disjoint
if they do not share an endpoint or an interior point. A
collection of pairwise disjoint edges is called a disjoint set. This notion is dual to that of a crossing set.
In the spirit of Turán's theorem, we can ask what is
the maximum number of edges that a geometric graph with
n
vertices can have without containing a disjoint set of size
k?
Hopf and Pannwitz [HP] proved that for
k = 2
the answer is
n.
This implies that Conways's Thrackle
Conjecture (mentioned above) is true for straight-line
thrackles. It had been a longstanding open problem of Erdos
and Perles whether the answer is at most
ckn,
for every
k,
before Pach and Törocsik settled this
question in the affirmative. In their argument,
ckn = O(k4)
Tóth and Valtr [TV] and Tóth [T] improved this
bound to
ckn = O(k3)
and
ckn = O(k2),
respectively. It is possible that
ckn
is linear in
k,
but this may be difficult to prove.
Results of this kind have interesting applications to the
Map Labelling Problems [AKS] arising in Geographic Information
Systems (GIS).
In a ground breaking series of papers, Pach and his co-authors
have started to develop the Ramsey Theory of Geometric and
Topological Graphs [KPT1,KPT2,KPT3,LMP,PSoT,PSo].
The prototype of the results in this area is that,
no matter how we color the edges of a
complete geometric graph with two colors, at least one of the
color classes will always contain a noncrossing spanning tree.
Results of this kind relate to deep problems for
partially ordered sets [Tr].
Bibliography
-
- AAP
-
P.K. Agarwal, B. Aronov, J. Pach, R. Pollack, M. Sharir:
Quasi planar graphs have linear number of edge,
Combinatorica 17 (1997), 1-9.
- AKS
-
P.K. Agarwal, M. Kreveld and S. Suri:
Label placement by maximum independent sets in rectangles,
Comput. Geometry:Theory and Appl.
11 (1998), 209-218.
- AC
- M. Ajtai, V. Chvátal, M. Newborn,
and E. Szemerédi: Crossing-free subgraphs,
Annals of Discrete Mathematics 12
(1982), 9-12.
- AE
-
N. Alon and P. Erdos:
Disjoint edges in geometric graphs,
Discrete Comput. Geom. 4 (1989), 287-290.
- AP
-
N. Alon and M. Perles: On the intersection of edges of a
geometric graph by straight lines,
Discrete Math. 60 (1986), 75-90.
- AEG
-
B. Aronov, P. Erdos, W. Goddard, D. J. Kleitman, D. J., M. Klugerman,
J. Pach and L. J. Schulman: Crossing families,
Combinatorica 14 (1994) 127-133.
- AH
- S. Avital and H. Hanani: Graphs, Gilyonot Lematematika 3 (1966), 2-8 (in Hebrew).
- BF
-
L. Babai and P. Frankl: Linear Algebra Methods in
Combinatorics, University of Chicago, 1988.
- BFP
-
I. Bárány, Z. Füredi, and J. Pach:
Discrete convex functions and proof of the six circle
conjecture of Fejes Tóth, Canad. J. Math. 36
(1984), 569-576.
- Be1
-
J. Beck:
On the lattice property of the plane and some problems of
Dirac, Motzkin and Erdos in combinatorial geometry,
Combinatorica 3 (1983), 281-297.
- Be2
- S. Benzer: On the topology of the genetic
fine structure,
Proceedings of the National Academy of Sciences of the
United States of America 45 (1959), 1607-1620.
- BL
- S. Bhatt and L. Leighton:
A framework for solving VLSI layout problems,
J. Comput. System Sci. 28 (1984), 300-331.
- B
- B. Bollobás: Extremal Graph Theory,
Academic Press, New York, 1978.
- C
-
F. R. Chung: The number of different distances determined
by n points in the plane, J. Combin. Theory Ser. A
36 (1984), 342-354.
- CST
- F. R. Chung, E. Szemerédi, and W.T.
Trotter: The number of different distances determined by
a set of points in the Euclidean plane, Discrete
and Computational Geometry 7 (1992), 1-11.
- CEG
-
K. Clarkson, H. Edelsbrunner, L. Guibas,
M. Sharir, and E. Welzl: Combinatorial
complexity bounds for arrangements of curves and spheres,
Discrete Comput. Geom. 5 (1990), 99-160.
- D
- T. K. Dey: Improved bounds for planar
k-sets
and related problems, Discrete and Computational
Geometry 19 (1998), 373-382.
- EG
-
P. Erdos and R. K. Guy:
Crossing number problems,
American Mathematical Monthly 80 (1973), 52-58.
- EH
-
P. Erdos and A. Hajnal:
Ramsey-type theorems,
Discrete Appl. Math. 25 (1989), 37-52.
- ELSS
-
P. Erdos, L. Lovász, A. Simmons, and E. G. Straus:
Dissection graphs of planar point sets,
in: A survey of combinatorial theory, Proc. Internat.
Sympos., Colorado State Univ., Fort Collins, Colo., 1971),
North-Holland, Amsterdam, 1973, 139-149.
- EGS
-
G. Even, S. Guha, and B. Schieber:
Improved approximations of crossings in graph Drawings,
in: Proc. 32nd Annual ACM Symposium on the Theory of
Computing (STOC 2000).
- FPP
- H. de Fraysseix, J. Pach, and R. Pollack:
How to draw a planar graph on a grid, Combinatorica
10 (1990), 41-51.
- GJ
- M. R. Garey and D. S. Johnson:
Crossing number is NP-complete,
SIAM Journal of Algebraic and Disccrete Methods
4 (1983), 312-316.
- Gr
- R. L. Graham: Problem,
in: Combinatorics, Vol. II (A. Hajnal and V. T. Sós,
eds.), North-Holland Publishing Company, Amsterdam, 1978,
1195.
- G
- R. K. Guy:
The decline and fall of Zarankiewicz's theorem,
in: Proof Techniques in Graph Theory, Academic Press,
New York, 1969, 63-69.
- G1
-
R. K. Guy: Latest results on the crossing number, in: Recent
Trends in Graph Theory,
Springer, New York (1971), 143-156.
- H
- A. Hanani (Ch. Chojnacki):
Über wesentlich unplättbare Kurven im dreidimensionalen
Raume, Fund. Math. 23 (1934), 135-142.
- HLS
-
H. van der Holst, L. Lovász, and A. Schrijver:
The Colin de Verdière graph parameter,
in: Graph theory and combinatorial biology (Balatonlelle, 1996),
Bolyai Soc. Math. Stud. 7, János Bolyai Math. Soc.,
Budapest, 1999, 29-85.
- HP
-
H. Hopf and E. Pannwitz:
Aufgabe No. 167, em Jahresbericht der deutschen
Mathematiker-Vereinigung 43 (1934), 114.
- KPT1
-
G. Károlyi, J. Pach, and G. Tóth: Ramsey-type
results for geometric graphs. I, in: ACM Symposium on
Computational Geometry (Philadelphia, PA, 1996). Also in:
Discrete Comput. Geom. 18 (1997), 247-255.
- KPT2
-
G. Károlyi, J. Pach, G. Tóth, and P. Valtr:
Ramsey-type results for geometric graphs. II,
in: ACM Symposium on Computational Geometry (Nice, 1997),
Discrete Comput. Geom. 20 (1998), 375-388.
- KPT3
-
G. Károlyi, J. Pach, G. Tardos, and G. Tóth:
An algorithm for finding many
disjoint monochromatic edges in a complete 2-colored
geometric graph, in: Intuitive Geometry (I. Bárány, K.
Böröczky, eds.) Bolyai Society Mathematical Studies
6, Budapest, 1997, 367-372.
- K
- D. König: Theorie der endlichen und
unendlichen Graphen, Leipzig, 1936. English translation:
Theory of Finite and Infinite Graphs, Birkhäuser
Verlag, Boston, 1990.
- KM
-
J. Kratochvíl and J. Matoušek: String graphs
requiring exponential representations, J. Combin. Theory
Ser. B 53 (1991), 1-4.
- Ku
- Y. Kupitz: Extremal problems in combinatorial
geometry, Aarhus University Lecture Notes Series 53,
Aarhus University, Denmark, 1979.
- LMP
- D. Larman, J. Matoušek, J. Pach, and
J. Törocsik: A Ramsey-type result for convex sets,
Bull. London Math. Soc. 26 (1994), 132-136.
- L
- T. Leighton:
Complexity Issues in VLSI, Foundations of Computing
Series, MIT Press, Cambridge, MA, 1983.
- LT
- R. J. Lipton and R. E. Tarjan: A separator theorem
for planar graphs, SIAM J. Appl. Math. 36 (1979),
177-189.
- Lo
- L. Lovász: On the number of halving lines,
Ann. Univ. Sci. Budapest. Eötvös Sect. Math.
14 (1971), 107-108.
- LPS
- L. Lovász, J. Pach, and M. Szegedy:
On Conway's thrackle conjecture,
Discrete and Computational Geometry 18 (1997),
369-376.
- P1
- J. Pach and P.K. Agarwal:
Combinatorial Geometry,
J. Wiley and Sons, New York, 1995.
- P2
- J. Pach: Geometric graph theory, in: Surveys in Combinatorics, 1999 (J. D. Lamb and D. A. Preece,
eds.), London Mathematical Society Lecture Note Series
267, Cambridge University Press, Cambridge, 1999,
167-200.
- P3
-
J. Pach: A problem of Ulam on planar graphs,
European J. Combin. 2 (1981), 357-361.
- PS
- J.Pach and M. Sharir: On the number of
incidences between points and curves,
Combinatorics, Probability and Computing 7
(1998), 121-127.
- PSS
- J. Pach, F. Shahrokhi, and M. Szegedy:
Applications of the crossing number,
Algorithmica 16 (1996), 111-117.
- PSo
-
J. Pach, J. Solymosi: Halving lines and perfect
cross-matchings, in: Advances in Discrete and
Computational Geometry (B. Chazelle, J.E. Goodman and
R. Pollack, eds.), Contemporary Mathematics 223
AMS, Providence, 1999, 245-249.
- PSoT
-
J. Pach, J. Solymosi, and G. Tóth:
Unavoidable configurations in complete topological graphs,
in: Graph Drawing 2000, Lecture Notes in Computer Science,
Springer-Verlag, accepted. Also in: Discrete and Computational
Geometry, submitted.
- PST
-
J. Pach, J. Spencer, and G. Tóth:
New bounds for crossing numbers,
Discrete and Computational Geometry 24 (2000),
623-644.
- PT
-
J. Pach and G. Tardos: Disentangling a polygon, in:
Abstracts of 963rd AMS Meeting, University of South
Carolina, Columbia, March 16-18, 2001, 17.
- PT0
-
J. Pach and J. Törocsik:
Some geometric applications of Dilworth's theorem,
Disc. Comput. Geometry 21 (1994), 1-7.
- PT1
- J. Pach and G. Tóth:
Graphs drawn with few crossings per
edge, Combinatorica 17 (1997), 427-439.
- PT2
- J. Pach and G. Tóth: Which crossing
number is it, anyway?, Proc. 39th Symp. on Foundation
of Computer Science, 1998, 617-626. Also in:
J. Combinat. Theory, Ser. B. 80 (2000), 225-246.
- PT3
- J. Pach and G. Tóth: String
representations of graphs, in:
Abstracts of 963rd AMS Meeting, University of South
Carolina, Columbia, March 16-18, 2001, 49.
- PW
- J. Pach and R. Wenger: Embedding planar
graphs at fixed vertex locations, in: Graph
Drawing (Montréal, QC, 1998),
Lecture Notes in Computer Science 1547, Springer,
Berlin, 1998, 263-274.
- RS
-
N. Robertson and P. Seymour:
Graph structure theory. Proceedings of the AMS-IMS-SIAM
Joint Summer Research Conference on Graph Minors
held at the University of Washington, Seattle, Washington,
June 22-July 5, 1991. Contemporary Mathematics 147,
American Mathematical Society, Providence, RI, 1993.
- RT
-
P. Rosenstiehl and R. Tarjan: Rectilinear planar layouts
and bipolar orientations of planar graphs,
Discrete Comput. Geom. 1 (1986), 343-353.
- SSS
-
F. Shahrokhi, O. Sýkora, L.A. Székely, and I. Vrto:
The book crossing number of graphs,
Journal of Graph Theory 21 (1996), 413-424.
- SoT
-
J. Solymosi and Cs. Tóth:
Distinct distances in the plane,
Discrete Comput. Geom., to appear.
- SW
- D. Souvaine and R. Wenger: Constructing
piecewise linear homeomorphisms, Comput. Geometry:
Theory and Appl.
- SST
- J. Spencer, E. Szemerédi, and W. T. Trotter, Jr.:
Unit distances in the Euclidean plane, in: Graph Theory and
Combinatorics (Cambridge, 1983), Academic Press, London, 1984,
293-303.
- S
- L. A. Székely: Crossing numbers and
hard Erdos problems in discrete geometry,
Combinatorics, Probability and Computing 6
(1997), 353-358.
- ST1
- E. Szemerédi and W. T. Trotter, Jr.:
Extremal problems in discrete geometry, Combinatorica
3 (1983), 381-392.
- ST2
-
E. Szemerédi and W. T. Trotter, Jr.: A combinatorial
distinction between the Euclidean and projective planes,
European J. Combin. 4 (1983), 385-394.
- T
- G. Tóth:
Note on geometric graphs,
J. Combin. Theory Ser. A 89 (2000), 126-132,
- TV
-
G. Tóth and P. Valtr,
Geometric graphs with few disjoint edges,
in: 14th Annual ACM Symposium on Computational
Geometry (Minneapolis, MN, 1998). Also in:
Discrete Comput. Geom. 22 (1999), 633-642.
- Tr
- W. T. Trotter, Jr.
Ramsey theory and partially ordered sets, in:
Contemporary trends in discrete mathematics (Štirín Castle, 1997),DIMACS Ser. Discrete Math.
Theoret. Comput. Sci. 49, Amer. Math. Soc., Providence, RI,
1999, 337-347.
- T1
- P. Turán: A note of welcome,
Journal of Graph Theory 1 (1977), 7-9.
- T2
- W. T. Tutte:
Toward a theory of crossing numbers,
Journal of Combinatorial Theory 8 (1970),
45-53.
- V
-
P. Valtr:
On geometric graphs with no
k pairwise parallel edges,
Disc. Comput. Geometry 19 (1998), 461-469.
- W
-
D. R. Woodall:
Thrackles and deadlock, in:
Combinatorial Mathematics and its Applications (Proc. Conf.,
Oxford, 1969), Academic Press, London, 1971, 335-347
|

