Implementing Addition and Subtraction

We wish to augment the ALU so that we can perform subtraction (as well as addition, AND, and OR).

• Big deal about 2's compliment is that
  A - B = A + (2's comp B)
  = A + (B' + 1).
• Get B' from an inverter (naturally).
• Get +1 from the Carry-In (clever).

A 1-bit ALU with ADD, SUB, AND, OR is shown on the right.

1. To implement addition we use opcode 10 as before and de-assert both b-invert and C_in.
2. To implement subtraction we still use opcode 10 but we assert both b-invert and C_in.

• For subtraction assert both B-invert and C_in.
• For addition de-assert both B-invert and C_in.
• For AND and OR de-assert B-invert. C_in is a don't care.
• We could get for A+B' (by asserting b-invert and de-asserting C_in)
  If we then let A=0, this gives B', i.e. the NOT operation
  However, we will not use it. Indeed we will soon give it away.

(More or less) all ALUs do AND, OR, ADD, SUB. Now we want to customize our ALU for the MIPS architecture, which has a few extra requirements.

1. slt set-less-than
2. Overflows
3. Zero Detect

Implementing SLT

This is fairly clever as we shall see.

• Result reg is 1 if a < b
  Result reg is 0 if a >= b
  
  
• So need to set the LOB (low order bit, aka least significant bit) of the result equal to the sign bit of a subtraction, and set the rest of the result bits to zero.
  
  
• Idea #1. Give the mux another input, called LESS. This input is brought in from outside the bit cell. That is, if the opcode is slt we make the select line to the mux equal to 11 (three) so that the the output is the this new input. For all the bits except the LOB, the LESS input is zero. For the LOB we must figure out how to set LESS.
  
• Idea #2. Bring out the result of the adder (BEFORE the mux)
  
  Only needed for the HOB (high order bit, i.e. sign) Take this new output from the HOB, call it SET and connect it to the LESS input in idea #1 for the LOB. The LESS input for other bits are set to zero.
  
  

• Why isn't this method used?
  
  
• Ans: It is wrong!
  
  
• Example using 3 bit numbers (i.e. -4 .. 3).
  • Try slt on -3 and +2.
  • True subtraction (-3 - +2) gives -5.
  • The negative sign in -5 indicates (correctly) that -3 < +2.
  • But three bit subtraction -3 - +2 gives +3 !
  • Hence we will incorrectly conclude that -3 is NOT less than +2.
  • (Really, the subtraction signals an overflow. unless doing unsigned)
  
  
• Solution: Need the correct rule for less than (not just sign of subtraction).
  
  

Implementing Overflow Detection

• The HOB ALU is already unique (outputs SET).
• Need to enhance it some more to produce the overflow output.
• Recall that we gave the rule for overflow. You need to examine:
  • Whether the operation is add or sub (binvert).
  • The sign of A.
  • The sign of B.
  • The sign of the result.
  • Since this is the HOB we have all the sign bits.
  • The book also uses Cout, but this appears to be an error.

Simpler Overflow Detection

Implementing Zero Detection

• To see if all bits are zero just need the NOR of all the bits
• Conceptually trivially but does require some wiring

The Final Result is

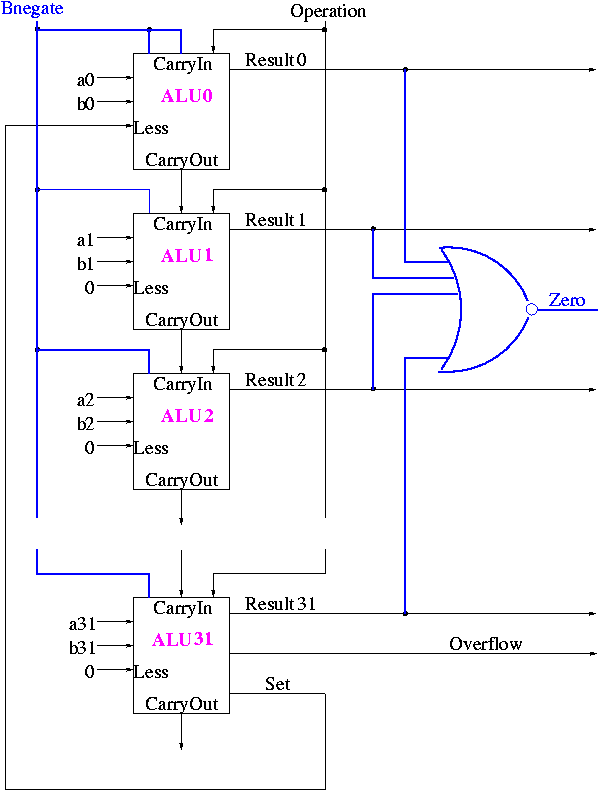
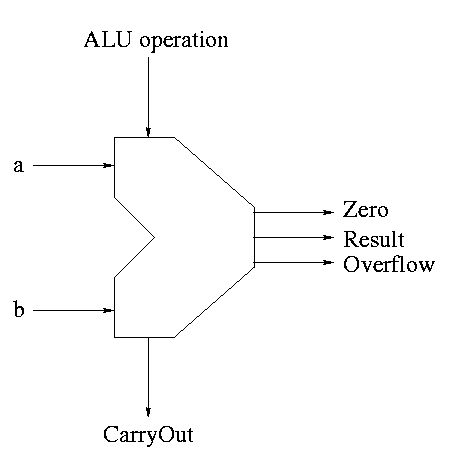
The symbol used for an ALU is on the right

What are the control lines?

• Bnegate (1 bit)
• OP (2 bits)

What functions can we perform?

• and
• or
• add
• sub
• set on less than

What (3-bit) values for the control lines do we need for each function? The control lines are Bnegate (1-bit) and Operation (2-bits)

and	0	00
or	0	01
add	0	10
sub	1	10
slt	1	11