GraphClust

Diego Reforgiato Recupero
Universita' di Catania
Dipartimento di Matematica e Informatica
diegoref@dmi.unict.it

Dennis Shasha
Courant Institute of Mathematical Sciences
Department of Computer Science
New York University
shasha@cs.nyu.edu

What is GraphClust?

GraphClust is a tool that, given a dataset of labeled (directed and undirected) graphs, clusters the graphs based on their topology. The GraphGrep software, by contrast, allows relatively small graphs to be used as queries into databases of usually larger graphs. That software finds matching subgraphs in the larger graphs very quickly.

GraphClust consists of 16 different algorithms broken down along four binary dimensions:

Number of clusters: The two options are: (1) specify the number of clusters explicitly. (The underlying algorithm is k-means neighbor.) (2) specify a "tightness" measure (an integer value in the range 1 to 4) where the higher the tightness value the smaller the cluster radius and hence the larger the number of clusters. (The underlying algorithm is the Antipole algorithm which is faster than k-means.)
Options: -kmeans k for k-means where k is an integer greater than 1 or -tightness k where k is between 1 and 4.
Default: Must be specified.
Definition of substructures: If the -s S option is specified then the comparison is based on the common substructures located by Subdue, developed at the University of Texas at Arlington, which finds common substructures in graphs. Otherwise, it looks for common paths up to a small length (currently 4). It works best with the -s S option.
Options: -s S for Subdue or -s P for paths
Default: Subdue.
Graph Type: Graphs can be either directed or undirected. If undirected, the edge specification is interpreted as a set of two-element sets as in LNE. If directed, the edge specification is interpreted as a set of ordered pairs.
Options: -g D for directed graph or -g U for undirected.
Default: undirected.
Distance metric: For each graph, we record the number of times each substructure is present, thus constituting a vector of non-negative integers. The metric between graphs is either (1) the inner product of the vectors for each graph; or (2) the Euclidean distance between those vectors.
Options: -m I for inner product or -m E for Euclidean.
Default: inner product.

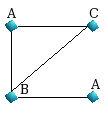
For all algorithms, the procedure starts in the same way. First, all substructures are found for each graph. Then a matrix A is formed whose columns consist of the union of all substructures and for which there is one row for each graph. Each entry A[i,j] represents the number of substructures j in graph i. The following example illustrates this when the substructures are paths, the graphs are considered to be undirected, the number of clusters is 15, and the distance metric is Euclidean. So the options would be -g U -m E -kmeans 15 -s S.

INPUT: graph1 and graph2


Graph 1	Graph 2

For Graph1, we have the following shortest paths of length 1 up to LP=3.
starting from the upper node A : {A,AC,AB,ABA}
starting from the node B : {B,BC,BA,BA}
starting from the downer node A : {A,AB,ABC,ABA}
starting from the node C : {C,CA,CB,CBA}

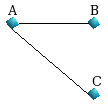
For Graph2, we have the following shortest paths of length 1 up to LP=3.
starting from the node A : {A,AB,AC}
starting from the node B : {B,BA,BAC}
starting from the node C : {C,CA,CAB}

When edges are undirected, the path XYZ is equal to path ZYX, and we form the following matrix A:

Graph	C	CA	CB	CBA	A	AB	ABA	B	BAC
Graph1	1	2	2	2	2	4	2	1	0
Graph2	1	2	0	0	1	2	0	1	2

Once the matrix A is created both algorithms take all rows and cluster them using distances - either inner product or Euclidean distance (Euclidean in this example), chosen by the user.
To use any algorithm of GraphClust you have to: (1) create a dataset file; (2) choose your options.
In addition, correlated (i.e. highly co-occurring) substructures pairs are displayed in descending order of correlation, as shown in the following example:

For each substructure, the nodes, painted as circles, have a label and an identification number. A circle containing the dot symbol is used as a dummy which means that the proposed substructure has only 1 node (the one linked to the circle with the dot symbol). Two input parameters are here involved:

-min m. Only substructures having at least m nodes are shown.
Options: integer value.
Default: 1.

-SVD r. When using SVD, the substructure-graph matrix A^T is broken apart into the product of 3 matrices T, S and D^T based on the singular value decomposition (SVD). These matrices are truncated to r dimensions. Dimensionality reduction reduces "noise" in the substructure-substructure matrix thus revealing a more robust relationship between the substructures. Finally, the substructure-substructure correlation matrix X is computed multiplying T_r×S_r×(T_r ×S_r)^T and its values are displayed.
Options: integer value.
Default: number of input graphs.

Let us consider the substructure-graph matrix A^T of the two graphs Graph1 and Graph2 showed above:

A^T=

Substructures	Graph1	Graph2
C	1	1
CA	2	2
CB	2	0
CBA	2	0
A	2	1
AB	4	2
ABA	2	0
B	1	1
BAC	0	2

The Singular Value Decomposition of A^T creates the following matrices T, S, D^T.

A^T=

-0.20	-0.17
-0.40	-0.33
-0.26	0.35
-0.26	0.35
-0.33	0.01
-0.66	0.02
-0.26	0.35
-0.20	-0.17
-0.13	-0.68

6.8	0
0	2.61

-0.89	0.46
-0.46	-0.89

D^T

Let us suppose the parameter r=1. The reduced matrices are T_r, S_r, D^T_r. Then, the reduced correlation substructure-substructure matrix X_r is equal to T_r×S_r×(T_r ×S_r)^T

X_r=

-0.20
-0.40
-0.26
-0.26
-0.33
-0.66
-0.26
-0.20
-0.13

6.8

× (

-0.20
-0.40
-0.26
-0.26
-0.33
-0.66
-0.26
-0.20
-0.13

6.8

)^T=

	C	CA	CB	CBA	A	AB	ABA	B	BAC
C	2	4	2	2	3	6	2	2	2
CA	4	8	4	4	6	12	4	4	4
CB	2	4	4	4	4	8	4	2	0
CBA	2	4	4	4	4	8	4	2	0
A	3	6	4	4	5	10	4	3	2
AB	6	12	8	8	10	20	8	6	4
ABA	2	4	4	4	4	8	4	2	0
B	2	4	2	2	3	6	2	2	2
BAC	2	4	0	0	2	4	0	2	4

T_r

S_r

× (

T_r

S_r

)^T

The output of "graphclust" includes a file named 'output' and a directory named 'correlation_files'.
The first one displays all the generated clusters and for each cluster it displays the centroid, all its elements and the distances of each element from the centroid.
The second one contains all the information pertaining to correlated substructures.

There are many applications for graph clustering. Some requests we have received have to do with Internet search engines, knowledge management systems, document databases and XML document management.

Home

Compare GraphClust

GraphClust is implemented in ANSI C, the graphical interface is implemented in JAVA and the substructure images are built by using the springgraph command.

Home

Download

To download GraphClust, please send email to shasha@cs.nyu.edu and to diegoref@dmi.unict.it.
If you care to describe your application, we'd be glad to hear about it. In any case, we will send you instructions for downloading the program.

Home

Installation of GraphClust

GraphClust is implemented in ANSI C. It has been ported on Unix, and Windows platforms.

To install GraphClust:

Unzip the GraphClust package
type "cd GraphClust"
type "cd src"
type "make"
type "cd .."
Check if there is "graphclust_main", "graphclustA", "graphclustA_S", "graphclustB", "graphclustB_S" existing in the current folder
Download the SubDue5.1 release from the download section at http://ailab.wsu.edu/subdue/
unzip the zip file where you want
go to subdue-5.1.0/src directory
type make
copy binary files sgiso and subdue to the directory that graphclust_main, graphclustA, graphclustA_S and graphclustB_S are in.
type ./graphclust_main without arguments to see all the possible options.
Check if the springgraph command is present in own unix system. (Even without it, the sotware still works but it will not show the substructures images).

For bugs and questions please contact diegoref@dmi.unict.it or shasha@cs.nyu.edu.

Home

Usage of GraphClust

File formats

dataset file
The file consists of a collection of graph specifications (LNE=List of Nodes and Edges ids format). The first line of each graph must begin with the character '#' and contains the label of the graph; it can be a number or a string. The next line contains the number of nodes in the graph. Subsequent lines contain the nodes' labels, one label per line. The first label is the label of node 0, the next one is the label of node 1, etc. Next is the number of edges in the graph, followed by a list of edges consisting of node id pairs. Each line contains only one edge. An example of dataset file is given in here.
output file
The output is given in a file called "output". Each Cluster is identified by an index number (starting from 1) with the number of graphs in the cluster and the radius in square brackets. In the next row we have the centroid of the cluster. In the subsequent rows we have the other elements, if any, and their distance from the centroid in brackets.
(see example here ).
The "correlation_files" directory includes all the information already showed in the form.

Running GraphClust

To run the examples go to the GraphClust directory and do the following

Execution
type graphclust_main dataset_file_name". You have to specify if you want to run the kmeans algorithm with the option -kmeans k where k is the number of clusters you want or with the Antipole algorithm with the option -tightness measure where measure is 1..4.
Other options are:
- -s S in order to use subdue algorithm to find the substructures
- -s P in order to use shortest path to find the substructures
- -g D to deal with directed graphs
- -g U to deal with undirected graphs
- -m I to use the inner product metric
- -m E to use the Euclidean distance
- -min m to show the substructures whose number of nodes is greater or equal than m
- -SVD r to reduce the substructure-substructure correlation matrix by using the SVD algorithm retaining the most r meaningful rows.

Home

Clustering References

Grant Support

This work has been partly supported by the U.S. National Science Foundation under grants IIS-0414763, DBI-0445666, N2010 IOB-0519985, N2010 DBI-0519984, DBI-0421604, and MCB-0209754. This support is greatly appreciated.