FinTime --- a financial time series benchmark

Kaippallimalil J. Jacob
Morgan Stanley Dean Witter & Co., New York (kjacob@acm.org)

&

Dennis Shasha
Prof, Computer Science Dept, Department of Computer Science
Courant Institute of Mathematical Sciences
New York University
Dennis Shasha's home page
(shasha@cs.nyu.edu)

FinTime home page

Time-series databases are of critical importance to finance and related applications. Many database vendors have made rapid progress in the implementation of these systems with increasing powerful capabilities and greater performance. Faced with a number of systems that claim support for time-series data it is quite difficult for a user to make an informed decision. Consequently, there is a need for a benchmark that characterizes these systems. The FinTime benchmark tries to model the practical uses of time-series databases in financial applications. FinTime will evolve with the help of vendors and customers..

• Data population, volume of data and update mechanism. Having defined the data model let us discuss the manner in which the data is fed to the database. Market information is typically provided as a set of input files by a market data vendor at the end of each trading day. These files correspond to the tables defined above. While the data for the Base Information table, Split Adjustment Table and Dividend Table is irregular (i.e. an external event triggers an entry into these tables), the Market Information Table has an entry for every trading day. For the purposes of this benchmark the implementation can select a scale factor combination of the number securities under consideration and the number of events for those securities. We suggest 3 scale factors, namely, 50,000 securities, 100,000 securities, and 1,000,000 securities, all for 4,000 days. These roughly correspond to all equity securities in the US, all equity securities in the G7 countries and all equity securities in the world. Programs to generate the data can be found here .

1. Response Time Metric: A single user metric

This can be defined as the geometric mean of the execution time of each of the queries executed one after the other in a single-user mode

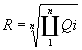Where Qi is the Execution time for query i

 

2. Throughput Metric: A multi-user metric

The Throughput Metric is defined as the average time taken by a user to complete his workload in a multi-user system.

Thus if Ei = total elapsed time for user "i" to execute the set of queries, then the throughput measure is define as

Where Ei = elapsed time to execute the set of queries for user i

3. Cost Metric. A cost measure

1. Full ACID property for transactions. This constraint is applicable to both models, where updates are applied concurrently with queries.
2. For either benchmark, each user must execute the complete query set once. They do not have the option of selecting a subset of queries or re-executing a query.

1. Transaction Processing Council (1998 ), "TPC-D Benchmark Specification" Version 2.0.
2. M. Stonebraker (1998), "Performance and Database Machines", Readings in Database Systems, Morgan-Kaufmann, San Mateo
3. D. Biiton, D. De Witt and C. Turbyfill (1983), "Benchmarking Database Systems: a systematic approach", Proceedings of the Ninth Very Large Database Conference, Florence, Italy
4. M. J. Carey, D. J. deWitt and J. F. Naughton (1993), "The OO7 Benchmark", Proceedings of the ACM SIGMOD International Conference on Management of Data, Washington D.C.
5. A. B. Chaudhri (1996), "An Annotated Bibliography of Benchmarks for Object Databases",

1. Split and Reverse Splits: A stock split is a process in which one share of a security is converted into a specified number of shares. A reverse split is the opposite process where a number of shares of a security is converted into 1 share. The ratio between the number of old securities and the new ones is called the split factor. E.g. If a security splits "2 for 1" the split factor is 0.5. If a security reverse splits "1 for 3" the split factor is 3/1 or 3.
2. Adjusted prices and volume. Since splits and reverse splits change the value of a security at the point the event occurs. E.g. Assume that an order to purchase 100 shares of a security at $50 per share was placed before a split. After a "2 for 1" split is effected, the order will be for 200 shares at $25. Notice that the total value of the order has not changes. However the price was multiplied by the split factor and the volume was divided it. A more comprehensive example follows. Consider the following snapshots of the split table and market info table for a specified security for a 1 week period.

Market Data

Date	OpenPrice	HighPrice	LowPrice	ClosePrice	Volume
1/3/99	100	110	90	105	10000
1/4/99	105	110	80	100	20000
1/5/99	50	55	50	55	20000
1/6/99	55	65	55	60	30000
1/7/99	60	80	60	75	50000
1/10/99	25	30	20	26	100000
1/11/99	26	36	20	34	150000

 

Splits Events

Date	SplitFactor	Comments
1/5/99	0.5	2 for 1 split
1/10/99	0.3333	3 for 1 split

 

Now the split-adjusted (or simply adjusted) prices and volumes for this given period would be as given in the following table

Date	OpenPrice	HighPrice	LowPrice	ClosePrice	Volume
1/3/99	16.67 (=100*0.5*0.33)	18.33 (=110*0.5*0.33)	15 (=90*0.5*0.33)	17.5 (=105*0.5*0.33)	60,000 (=10,000*2*3)
1/4/99	17.5 (=105*0.5*0.33)	18.33 (=110*0.5*0.33)	13.33 (=80*0.5*0.33)	16.67 (=100*0.5*0.33)	120,000 (=20,000*2*3)
1/5/99	16.67 (=50*0.33)	18.33 (=55*0.33)	16.67 (=50*0.33)	18.33 (=55*0.33)	60,000 (=20,000 * 3)
1/6/99	18.33 (=55*0.33)	21.67 (=65*0.33)	18.33 (=55*0.33)	20 (=60*0.33)	90,000 (=30,000 * 3)
1/7/99	20 (=60*0.33)	26.67 (=80*0.33)	20 (=60*0.33)	25 (=75*0.33)	150,000 (=50,000 * 3)
1/10/99	25	30	20	26	100,000
1/11/99	26	36	20	34	150,000

 

3. Volume-weighted price: This measure is a weighted average of the trade prices where the size of each trade is used as the weight. The following example illustrates the concept:

Tdate	Time	TradePrice	TradeSize
1/5/99	10:00a	100	100
1/5/99	10:10a	101	500
1/5/99	10:15a	100.5	1000
1/5/99	10:20a	99	200
1/5/99	10:25a	98	300
1/5/99	10:30a	100	400
1/5/99	10:35a	99	500
1/5/99	10:45a	98	600
1/5/99	10:55a	99	700

Table A2.3

 

Now Volume Weighted Price (VWP) is defined as :



Therefore in the above example, the VWP for all trades shown in the table is



 

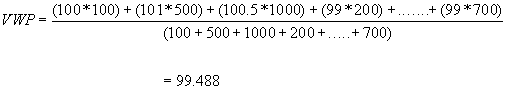
4. Standard Industry Code: Most market data vendors provide a categorization of securities by the industry in which they operate. For example, IBM is categorized to be in the "COMPUTERS" business. While typically they are codes, in this benchmark we have expanded them in meaningful words.
5. Dividends & Yield: Dividends are pay-outs of earnings to shareholders. They are specified as a dollar amount per share and the date of disbursement is termed as the Ex-Dividend date. Dividends may be paid out per quarter or annually or according to any other schedule that the company chooses. Annual Yield for a security, as defined for this benchmark, is the total dividend paid out during a calendar year as a percentage of the average share price (split adjusted). It is important to note that dividend payments should also be split adjusted (dividend rate * split factor).
6. n-Day Moving Average: This is simple statistic wherein a n-day sliding window is moved over the time period in question from the start date to the end day. The average value (price) is calculate for each position of the window and the calculated value is associated with the last date in the window. E.g Consider the split adjusted prices in Table A2.3. The 3-day moving average for the closing price would be as follows:

Date	Moving Avg-ClosingPrice	Comments
1/5/99	17.5	Avg(17.5, 16,67, 18.33)
1/6/99	18.33	Avg(16.67, 18.33, 20)
1/7/99	21.11	Avg(18.33, 20, 25)
1/10/99	23.67	Avg(20, 25, 26)
1/11/99	28.33	Avg(25, 26, 34)

 

7. Spread: is defined to be the difference between the price at which a broker will sell a security and the price at which the broker will buy it. This is the source of profits for a broker. Typically, large well recognized securities have small spread while securities of small companies have larger spreads.
8. Coefficient of correlation for two sequences is defined as: the covariance over the product of the standard deviations. If x and y are vectors, then the covariance is covariance(x,y) = avg(x * y) - (avg(x)*avg(y)) correlation coefficient = covariance(x * y) / (stddev(x)*stddev(y)) where avg is average, stddev is the standard deviation.
9. The notions of ``specified period of x days'' or ``set of y securities'' are used in the query descriptions. To compute a specified period of x days from a set of days D, choose x days without replacement randomly and uniformly from D. If they must be consecutive days, then choose a single day randomly and uniformly from the set of days that are at least x less than the most recent day in the database. The same holds for hours in the tick database. To compute a set of x securities from some set S, choose the x randomly and uniformly but without replacement from S.
10. S&P/Russell indices. The composition of these indexes can be generated by randomly selecting 500 and 2000 distinct securities at random uniformly and without replacement from the universe of securities.
11. Data Types. Data types for the data models described above are as follows: